Symmetrisches Matrizeneigenwertproblem (Bsp.)
 Im Kapitel 29 des Lehrbuchs
"Dankert/Dankert:
Technische Mechanik"
wird folgende Aufgabe formuliert:
Im Kapitel 29 des Lehrbuchs
"Dankert/Dankert:
Technische Mechanik"
wird folgende Aufgabe formuliert:
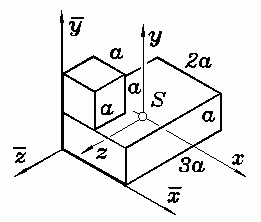
Für den aus einem Quader und einem Würfel zusammengesetzten homogenen Körper sollen die Lage der Hauptzentralachsen und die zugehörigen Hauptträgheitmomente ermittelt werden.
Gegeben: a , Dichte ρ .
Nach einigen (recht mühsamen) Vorarbeiten (Berechnung der Lage des Schwerpunkts und Berechnung aller Trägheitsmomente bezüglich des eingezeichneten Schwerpunktkoordinatensystems) kann der Trägheitstensor bezüglich des x-y-z-Koordinatensystems aufgeschrieben werden (enthät die drei Massenträgheitsmomente Jxx, Jyy und Jzz und die drei Deviationsmomente Jxy, Jxz und Jyz):
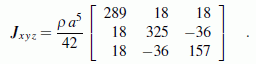
Die Eigenwerte dieser Matrix sind die Hauptträgheitmomente, ihre Eigenvektoren definieren die Lage der Hauptzentralachsen.
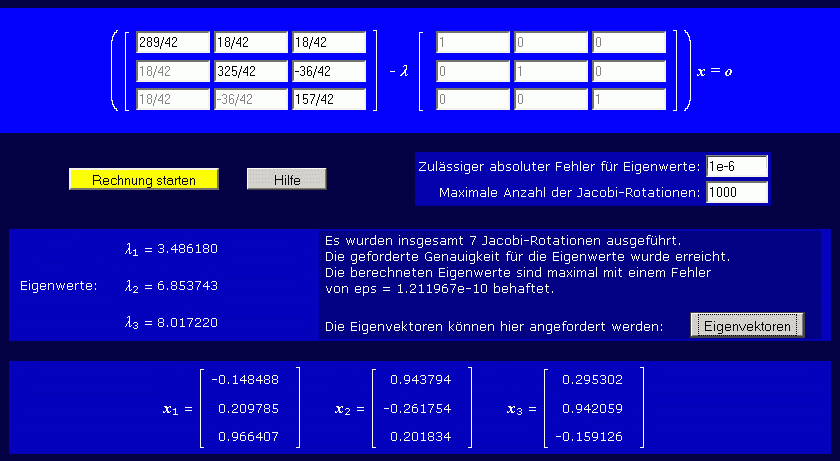
Nach dem Start des Programms "Symmetrisches Matrizeneigenwertproblem" können alle Voreinstellungen (spezielles Matrizeneigenwertproblem für eine Matrix mit 3 Zeilen/Spalten) beibehalten werden. Bei der Eingabe der Matrix bleibt der Faktor ρa5 unberücksichtigt (die berechneten Eigenwerte müssen dann noch mit diesem Faktor multipliziert werden), der Nenner (die Zahl 42) wird in die Matrix hineingenommen. Nach Eingabe der Werte wird zunächst "Rechnung starten" angeklickt (die Eigenwerte werden berechnet), danach wird auch noch das danach erscheinende Angebot "Eigenvektoren" ausgewählt, und der Bildschirm müsste so aussehen:
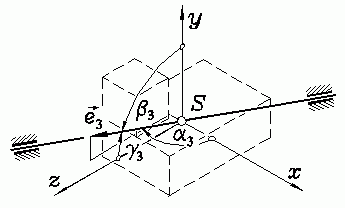
Für Interessenten soll noch erläutert werden, was da eigentlich berechnet wurde: Die Eigenvektoren kennzeichnen die Richtungen der drei Hauptzentralachsen, was an einem Beispiel deutlich gemacht wird: Der zum kleinsten Eigenwert (kleinstes Hauptträgheitsmoment) gehörende Eigenvektor x1 enthält die Richtungskosinusse, die die zugehörige Hauptzentralachse definieren. Weil es in der Technischen Mechanik üblich ist, die Achse des größten Hauptträgheitsmoments mit dem Index 1 und die des kleinsten Hauptträgheitsmoments mit dem Index 3 zu bezeichnen, wurde dem Einheitsvektor, der durch x1 festgelegt wird, in der nebenstehenden Skizze und in folgender Formel der Index 3 gegeben:
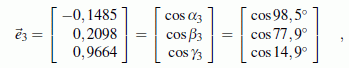
Bezüglich dieser Achse gilt also das kleinste Hauptträgheitsmoment
Das kleinste der drei Hauptträgheitsmomente bezüglich der Schwerpunktachsen ist immer das kleinste Massenträgheitsmoment des Körpers überhaupt (wegen der immer positiven Steiner-Anteile der axialen Massenträgheitsmomente haben alle parallelen Achsen größere Trägheitsmomente). Die in der Abbildung eingezeichnete Drehachse ist für diesen Körper also die Achse mit der geringsten Drehträgheit.
Nur bei Rotation um eine der drei Hauptzentralachsen (im Beispiel durch die drei Eigenvektoren definiert) werden die Lager ausschließlich durch die Gewichtskraft der Masse (und eventuell weitere äußere Kräfte) und nicht durch die Trägheitskräfte der Bewegung belastet ("Der Körper rotiert stabil.").