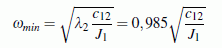Symmetrisches Matrizeneigenwertproblem (Bsp.)

Im Kapitel 32 des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird folgende Aufgabe formuliert:

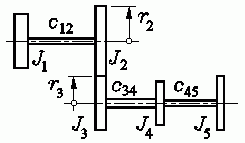Für das skizzierte Getriebe mit fünf (starren) Rädern und drei (masselosen) Torsionsfedern (Wellenabschnitte) soll das Matrizeneigenwertproblem für die Berechnung der Eigenkreisfrequenzen der Torsionsschwingungen formuliert werden. Es darf vorausgesetzt werden, dass die beiden Zahnräder mit den Massenträgheitsmomenten J₂ und J₃ und den Teilkreisradien r₂ und r₃ spielfrei miteinander kämmen.

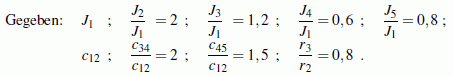
Das Schwingungs-Differenzialgleichungssystem führt nach nicht sehr schwieriger Rechnung auf folgendes Matrizeneigenwertproblem:

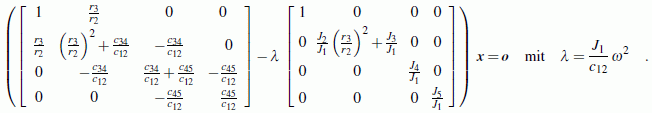
Die Eigenwerte dieses allgemeinen Matrizeneigenwertproblems sind also dem Quadrat der Eigenkreisfrequenzen proportional.

Nach dem Start des Programms "Symmetrisches Matrizeneigenwertproblem" werden zunächst die gegebenen Größen als Konstanten definiert (über die beiden gelben Eingabefelder links oben). Dabei werden "sprechende Namen" verwendet (zum Beispiel J2dJ1 für "J₂ durch J₁"). Der Bildschirm-Ausschnitt rechts zeigt die Situation, nachdem bereits sechs Konstanten definiert sind und die Definition der siebten Konstanten r3dr2 vorbereitet ist. Mit Enter oder Anklicken von "Neue Konstante" wird eine Konstanten-Definition abgeschlossen.

Als Eingabeschema wird "... allgemeines Matrizeneigenwertproblem" gewählt und für die Zeilen-/Spalten-Anzahl wird n = 4 eingegeben:

Nach Anklicken von "OK" erweitert sich das Eingabeschema entsprechend, und die Matrixelemente können unter Verwendung der definierten Konstanten eingegeben werden. Dabei müssen nur die Elemente des rechten oberen Dreiecks definiert werden, die dazu symmetrischen Elemente entstehen automatisch.

Wenn die Eingabe komplett ist, kann "Rechnung starten" angeklickt werden, und die Eigenwerte erscheinen. Wenn außerdem die angebotene Offerte "Eigenvektoren" gewählt wird, müsste der Bildschirm schließlich so aussehen:

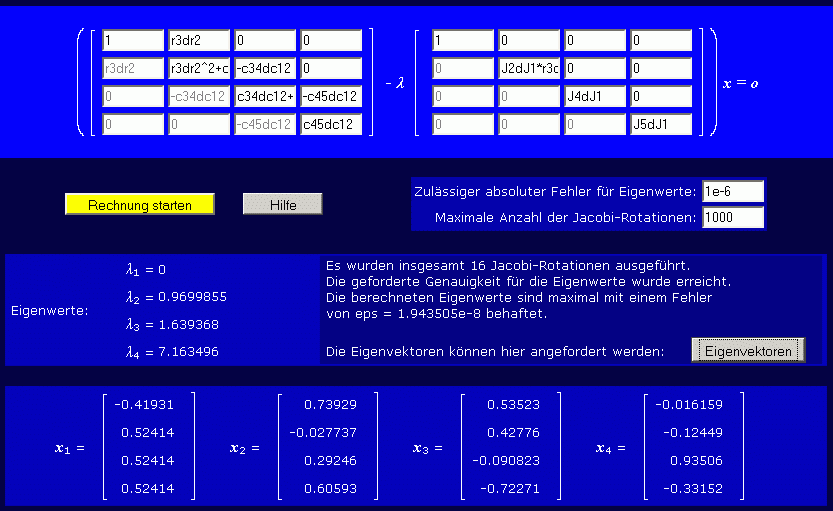
Für Interessenten soll noch erläutert werden, was da eigentlich berechnet wurde:

• Die jeweils vier Komponenten der Eigenvektoren sind die Verdrehwinkel der Räder 1, 3, 4 und 5. Der Verdrehwinkel des Rades 2 wurde eliminiert, weil sein Betrag stets das 0,8-fache des Verdrehwinkels des Rades 3 sein muss.
• Der kleinste Eigenwert λ₁ = 0 (entspricht einer Eigenkreisfrequenz ω₁ = 0) ist typisch für die Berechnung der Torsionsschwingungen von Getrieben. Darin drückt sich die Möglichkeit der Starrkörperbewegung aus (Bewegung, bei der sich die Getriebeglieder nicht verformen müssen). Darin liegt der eigentliche Sinn eines Getriebes. Der zugehörige Eigenvektor zeigt das: Die letzten drei Werte gehören zu den Rädern 3, 4 und 5 und sind bei der Starrkörperbewegung gleich. Der erste Wert kennzeichnet die Verdrehung der Räder 1 und 2, das andere Vorzeichen kennzeichnet die entgegengesetzte Drehrichtung, in den absoluten Werten steckt das Übersetzungsverhältnis von Rad 3 zu Rad 2.
• Eigenkreisfrequenzen von Torsionsschwingungen werden also nur von den Eigenwerten λ₂, λ₃ und λ₄ beschrieben. Zum kleinsten Wert
  
  gehört der 2. Eigenvektor, bei dem die Verdrehwinkel der Räder 3 und 4 unterschiedliche Vorzeichen haben. Zwischen diesen beiden Rädern liegt also ein Schwingungsknoten.