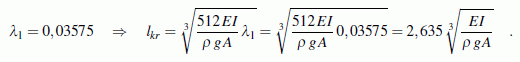Symmetrisches Matrizeneigenwertproblem (Bsp.)

Im Kapitel 23 des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird folgende Aufgabe formuliert:

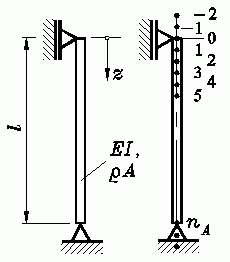
Der skizzierte Stab ist nur durch sein Eigengewicht belastet. Es soll ermittelt werden, bei welcher kritischen Länge er allein durch die Eigengewichts-Belastung knickt.

Gegeben:   EI ,   Dichte ρ ,   Querschnittsfläche A .

Die Lösung wird mit dem Differenzenverfahren auf der Basis der Differenzialgleichung 4. Ordnung für den Knickstab erreicht: Der Stab wird in n_A äquidistante Abschnitte unterteilt, es entstehen n_A − 1 Punkte im Inneren des Stabs, für die die Differenzenformeln aufgeschrieben werden. In diese Gleichungen gehen auch die Rand- und Außenpunkte ein, die mit Hilfe der Randbedingungen eliminiert werden können.

Dieser Weg wird im Lehrbuch ausführlich beschrieben. Nach etwas mühsamer (aber nicht sehr schwieriger) Rechnung entsteht ein Matrizeneigenwertproblem. Für n_A = 8 sieht es zum Beispiel so aus:

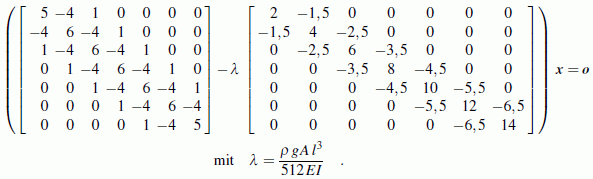
Nach dem Start des Programms "Symmetrisches Matrizeneigenwertproblem" wird als Eingabeschema "... allgemeines Matrizeneigenwertproblem" gewählt und für die Zeilen-/Spalten-Anzahl wird n = 7 eingegeben:

Nach Anklicken von "OK" erweitert sich das Eingabeschema entsprechend, und die Matrizen können eingegeben werden. Danach wird "Rechnung starten" gewählt, und der Bildschirm sollte so aussehen:

Die oben angegebene Formel für λ wird nach l umgestellt. Wenn dann der kleinste Eigenwert eingesetzt wird, erhält man die gesuchte kritische Stablänge: