Beispiel zum Programm Anfangswertproblem

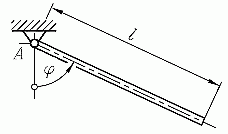Ein dünner Stab der Länge l mit konstantem Querschnitt ist an einem Ende reibungsfrei gelagert. Er wird aus der vertikalen Lage um den Winkel φ₀ ausgelenkt und ohne Anfangsgeschwindigkeit freigegeben (Luftwiderstand kann vernachlässigt werden).

Gegeben:  l = 1 m ;  Erdbeschleunigung g = 9,81 m/s² ,  φ₀ = 3π/4.

Es sind die Bewegungsgesetze φ(t) und ω(t) für die ersten 10 Sekunden der Bewegung zu ermitteln.

Im Kapitel 29 des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird das Anfangswertproblem für diese Aufgabe hergeleitet:

Dieses Anfangswertproblem 2. Ordnung kann durch Einführen einer neue Variablen ω für die erste Ableitung von φ in ein Anfangswertproblem 1. Ordnung überführt werden, das in dieser Form dem Programm "Anfangswertproblem" angeboten werden kann:

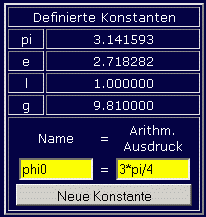
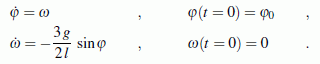
Nach dem Start des Programms "Anfangswertproblem" werden zunächst die gegebenen Parameter als Konstanten definiert. Rechts sieht man die Tabelle mit den beiden vordefinierten Konstanten pi und e und den bereits definierten Konstanten l und g. Im gelben Bereich sieht man die Vorbereitung der Definition von phi0, und nach Klick auf "Neue Konstante" ist die Konstantendefinition abgeschlossen.

Die Voreinstellungen für den Integrationsbereich (t_anf, t_end, n_steps) können beibehalten werden, so dass man mit der Definition der Differenzialgleichungen fortfahren kann. Wenn phi' in das Feld "Name" eingetragen wird, bietet das Programm im rechten Bereich dieser Zeile gleich das dazu passende Schema für die zugehörige Anfangsbedingung an. Nach Eintragen des erweiterten arithmetischen Ausdrucks (in diesem Fall nur: omega) und Ergänzen der Anfangsbedingung (phi0) sieht die Eingabezeile so aus:

Nach Anklicken von "OK" kann die zweite Differenzialgleichung definiert werden:

Damit ist die Eingabe des Anfangswertproblems abgeschlossen. Es wurde unterhalb des Eingabebereichs protokolliert. Vor der Berechnung sollte immer das Angebot "Syntaxcheck" genutzt werden. Nach Anklicken des entsprechenden Buttons sieht das Eingabeprotokoll so aus:

Nun kann der Button "Berechnung starten" angeklickt werden. Als Ergebnisse erscheinen zunächst die Werte für φ(t_end) und ω(t_end) und die grafische Darstellung von φ(t) und ω(t) über den gesamten Integrationsbereich:

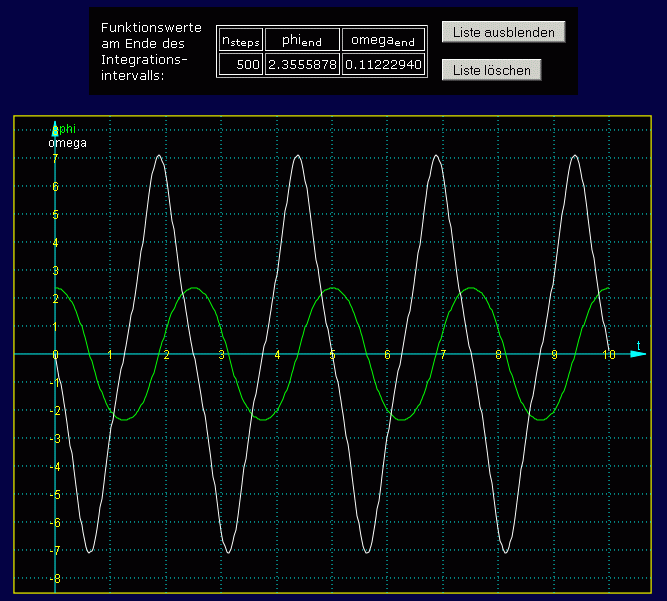
Kontrolle der Ergebnisse: Die grafische Darstellung der Funktionen φ(t) und ω(t) entspricht den Erwartungen. Weil keine Reibungsverluste entstehen, müssen die Mimima und Maxima stets wieder den gleichen Wert erreichen. Die visuelle Kontrolle bestätigt das.

Man sollte grundsätzlich mindestens eine zweite Rechnung mit einer größeren Schrittanzahl durchführen und die Endwerte vergleichen, die im Programm gesammelt werden. Nachfolgend sieht man diese Werte für insgesamt 4 Rechnungen mit unterschiedlicher Schrittanzahl:

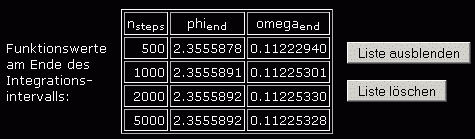
Die Werte ändern sich nur unbedeutend. Selbst die erste Rechnung mit n_steps = 500 genügt auch gehobenen Genauigkeitsanforderungen.

Zusätzlich sollen noch zwei physikalische Kontrollmöglichkeiten demonstriert werden, die hier möglich sind, weil keine Energieverluste während der Bewegung auftreten. Im Skript "Numerische Integration von Anfangswertproblemen, Teil 1" wird gezeigt, dass die Gesamtenergie des Systems T_ges in einer beliebigen Lage durch folgende Formel beschrieben wird (Nullpotenzial liegt auf dem Niveau des Lagerpunktes), hier umgeschrieben auf eine dimensionslose Form:

Diese Funktion wird zusätzlich definiert:

Um die Auswirkungen von Fehlern überhaupt erkennen zu können, wird wieder die Standardeinstellung n_steps = 500 eingestellt. Nachdem "Berechnung starten" angeklickt wurde, ändert sich zunächsts nichts, denn standardmäßig werden nur die Funktionen grafisch dargestellt, die Lösungen von Differenzialgleichungen sind.

Unterhalb der Grafik findet man ein blaues Feld, mit dem die Art der grafischen Darstellung festgelegt wird. Zunächst wird die Anzahl der Grafikfenster (Standardeinstellung: 1) auf 4 erhöht (1, 2 oder 4 sind möglich). Das blaue Feld erweitert sich entsprechend, folgende Änderungen werden vorgenommen: Im Grafikfenster 1 (links oben) soll nur noch φ(t) dargestellt werden, im Grafikfenster 3 (links unten) ω(t), was jeweils durch entsprechende Änderung im Eingabefeld "Funktionen" realisiert wird. Im Graphikfenster 2 (rechts oben) soll ω(φ) dargestellt werden, dafür muss im Feld "Abszisse" phi eingetragen werden (Standard ist t). Im Grafikfenster 4 schließlich soll die Funktion T(t) dargestellt werden. So muss das Feld dann aussehen:

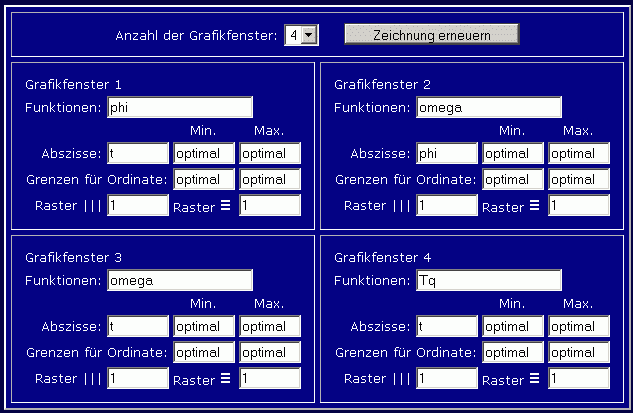
Nach Anklicken des Buttons "Zeichnung erneuern" sieht die Grafik so aus:

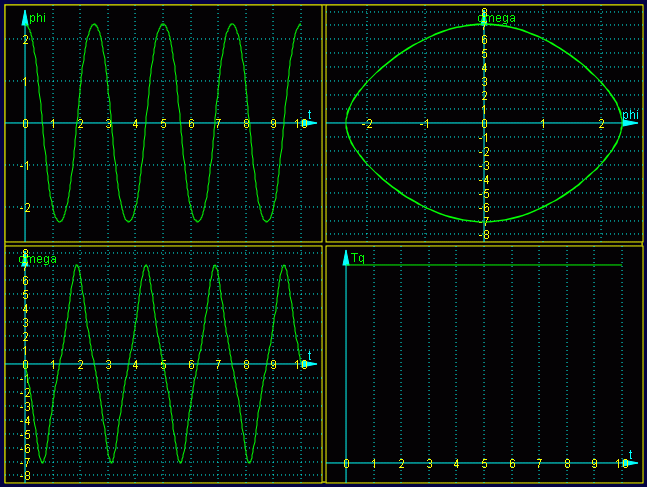
Folgende Indizien zeigen, dass die Rechnung "gesund" ist:

• Die Funktion ω(φ) im Fenster rechts oben (Darstellung in der so genannten "Phasenebene") zeichnet bei der Darstellung von etwa vier vollen Schwingungen die Kurven vierfach übereinander. Die Linie erscheint dadurch etwas breiter, aber bei einer ungenauen Rechnung wären deutliche Abweichungen zu sehen.
• Die Funktion T(t) im Fenster rechts unten zeigt die erwartete horizontale Linie (kein Energieverlust während der Bewegung).

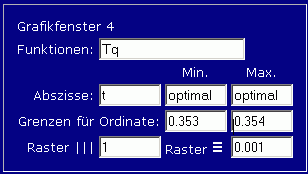
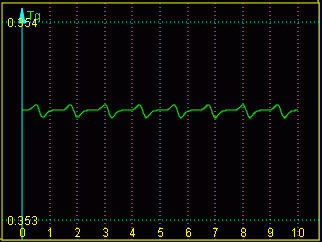
Die "schöne horizontale Kurve" der Funktion T(t) zeigt allerdings bei einem extremen Zoom durchaus Fehler: Mit den Einstellungen für Grafikfenster 4, die links zu sehen sind, zeigt diese Grafik, dass es doch Abweichungen gibt.

Dies verdeutlicht allerdings ein grundsätzlich nicht zu beseitigendes Problem der numerischen Integration von Anfangswertproblemen: Man kann die Fehler durch kleinere Schrittweiten (oder auch durch Verwendung besserer Integrationsformeln) sehr stark verkleinern, aber ein immer stärkerer Zoom wird eine solche theoretisch ideale Gerade immer zu einer Kurve werden lassen, die der hier dargestellten ähnlich ist.