Beispiel zum Programm Anfangswertproblem

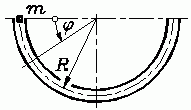Ein Massenpunkt m wird wie skizziert in eine halbkreisförmige Rinne gelegt und ohne Anfangsgeschwindigkeit freigegeben. Das Bewegungsgesetz φ(t) soll bei Berücksichtigung der Gleitreibung zwischen Massenpunkt und Rinne für die ersten 10 Sekunden der Bewegung berechnet werden.

Gegeben:  R = 1 m ;  Erdbeschleunigung g = 9,81 m/s² ;  μ =0,05 .

Im Kapitel 28 des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird das Anfangswertproblem für diese Aufgabe hergeleitet:

Das Problem steckt im zweiten Term der Differenzialgleichung: Weil bei Umkehr der Bewegungsrichtung die Reibkraft auch ihre Richtung ändert, wurde die Signum-Funktion verwendet (mit der Winkelgeschwindigkeit als Argument). Zunächst wird das Anfangswertproblem 2. Ordnung durch Einführen einer neue Variablen ω für die erste Ableitung von φ in ein Anfangswertproblem 1. Ordnung überführt:

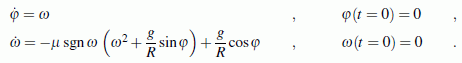
Der Ausdruck vor der Klammer wird als neue Funktion μ_t betrachtet, für die folgende Definition gilt:

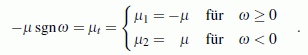
Die Voreinstellungen für den Integrationsbereich (t_anf, t_end, n_steps) können beibehalten werden. Zunächst werden die gegebenen Größen als Konstanten definiert (nebenstehendes Bild). Vor der Definition der Differenzialgleichungen werden die Funktionen my1, my2 (jeweils mit den oben angegebenen Gültigkeitsbereichen) und myt definiert. Weil im Programm "Anfangswertprobleme" Funktionen außerhalb ihres Gültigkeitsbereichs den Wert 0 haben, kann myt einfach als Summe aus my1 und my2 definiert werden. Wenn my1 in das Feld "Name" eingetragen wird, bietet das Programm im rechten Bereich dieser Zeile gleich das dazu passende Schema für den zugehörigen Gültigkeitsbereich an. Die komplett ausgefüllte Zeile sieht dann so aus:

Wenn der Eintrag in das Feld "Name" mit dem Zeichen ' abgeschlossen wird, dann wird neben der Definition einer Differenzialgleichung auch noch die zugehörige Anfangsbedingung abgefordert, zum Beispiel:

Alle eingegebenen Funktionen und Differenzialgleichungen werden unterhalb des Eingabebereichs protokolliert. Vor der Berechnung sollte immer das Angebot "Syntaxcheck" genutzt werden. Nach Anklicken des entsprechenden Buttons sieht das Eingabeprotokoll so aus:

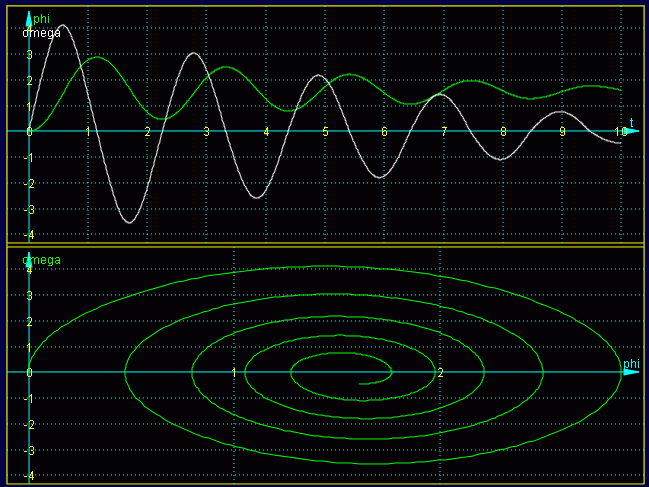
Nun kann der Button "Berechnung starten" angeklickt werden. Als Ergebnisse erscheinen zunächst die Werte für φ(t_end) und ω(t_end) und die grafische Darstellung von φ(t) und ω(t) über den gesamten Integrationsbereich:

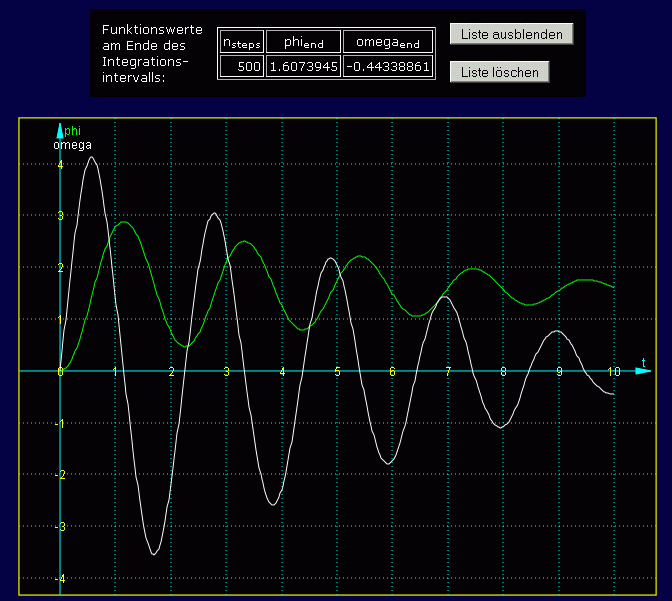
Man sollte grundsätzlich mindestens eine zweite Rechnung mit einer größeren Schrittanzahl durchführen und die Endwerte vergleichen, die im Programm gesammelt werden. Nach einer zweiten Rechnung mit n_steps = 1000 sieht die Liste so aus:

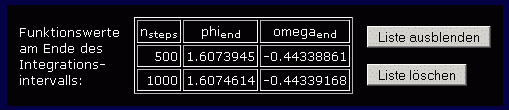
Die Werte ändern sich nur unbedeutend, die Genauigkeit ist also ausreichend.

Unterhalb der Grafik findet man ein blaues Feld, mit dem die Art der grafischen Darstellung festgelegt wird. Hier soll nur zusätzlich die Funktion ω(φ) in einem zweiten Fenster dargestellt werden. Zunächst wird die Anzahl der Grafikfenster (Standardeinstellung: 1) auf 2 erhöht (1, 2 oder 4 sind möglich). Das blaue Feld erweitert sich entsprechend, folgende Änderungen werden vorgenommen: Im Grafikfenster 2 wird im Feld "Funktionen" omega eingetragen, im Feld "Abszisse" wird phi eingetragen.

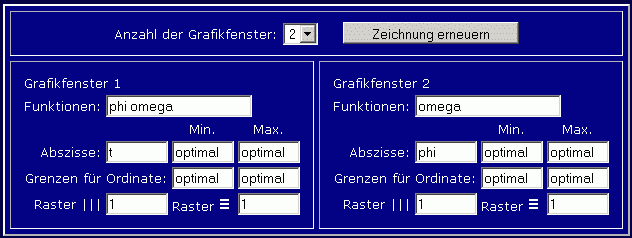
Nach Anklicken des Buttons "Zeichnung erneuern" sieht die Grafik so aus: