Überbestimmtes Gleichungssystem - Beispiel

Im Kapitel 6 des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird folgende Aufgabe formuliert:

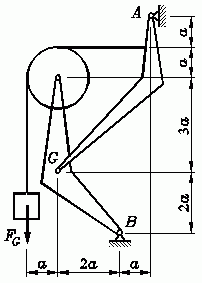
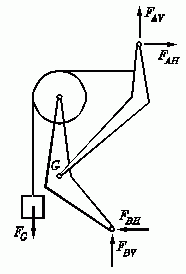
Das skizzierte zusammengesetzte System ist durch die Gewichtskraft F_G der an einem Seil hängenden Masse belastet. Man ermittle die durch F_G hervorgerufenen Lagerreaktionen bei A und B und die Gelenkkraftkomponenten im Gelenk G.

Gegeben:  a ,   F_G .

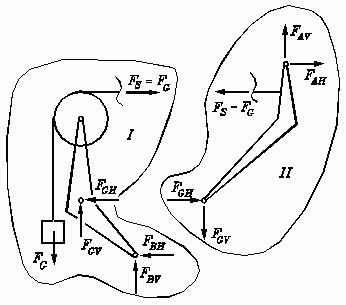
Das System wird entsprechend der Schnittskizze in zwei Teilsysteme zerlegt, an denen die insgesamt 6 unbekannten Kräfte (F_AH, F_AV, F_BH, F_BV, F_GH, F_GV) aus 6 Gleichgewichtsbedingungen berechnet werden können.

Die Abmessung a kürzt sich aus allen Gleichungen heraus, und die Gleichgewichtsbedingungen lassen sich schließlich zu einem linearen Gleichungssystem zusammenfassen, in dem die Kraft F_G als gemeinsamer Faktor auf der rechten Seite steht, so dass auch dafür kein Zahlenwert für eine numerische Lösung erforderlich ist (man muss natürlich alle Ergebnisse mit F_G multiplizieren). Das sich ergebende Gleichungssystem wird hier gleich in Matrixform zusammengefasst:

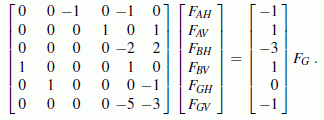
Weil die Anzahl der Unbekannten mit der Anzahl der Gleichungen übereinstimmt, könnte es auch mit dem Programm "Lineares Gleichungssystem, Matrixinversion" berechnet werden. Aber auch das Programm "Überbestimmtes lineares Gleichungssystem" lässt diesen Sonderfall zu, wenn man m = n setzt:

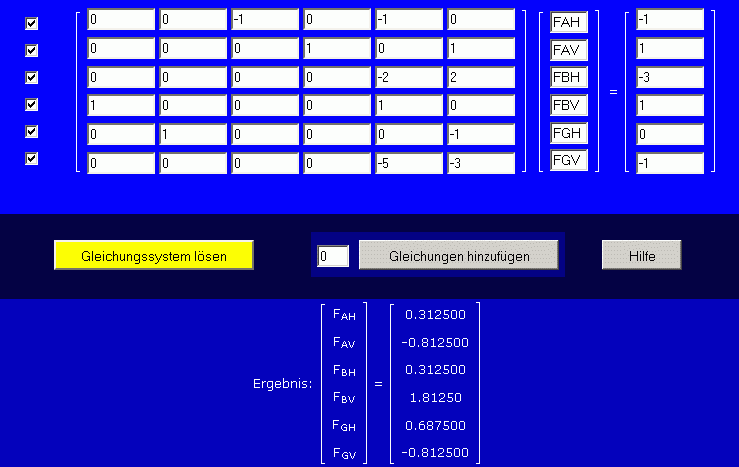
Nach Eingabe des Gleichungssystems in das Eingabeschema wird "Gleichungssystem lösen" angeklickt, und Gleichungssystem und Ergebnis sollten so aussehen:

Weil diese Berechnungen in jedem Fall fehleranfällig sind, werden in der Technischen Mechanik immer zusätzliche Gleichgewichtsbedingen als Kontrollgleichungen empfohlen. Es bietet sich an, bei Arbeit mit Teilsystemen (wie in diesem Fall zwingend) auch noch die Gleichgewichtsbedingungen am Gesamtsystem zu formulieren. Rechts sieht man dieses System, das nur von den äußeren Bindungen (Lager) gelöst wurde. An diesem System werden drei Gleichgewichtsbedingungen formuliert (Summe aller Horizontalkräfte, Summe aller Vertikalkräfte und Summe aller Momente um das Lager B):

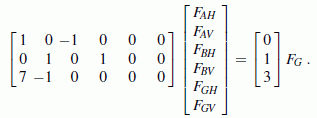
Diese Gleichungen können dem Programm zusätzlich angeboten werden, indem in das Feld vor dem Button "Gleichungen hinzufügen" die Zahl 3 eingetragen und anschließend dieser Button angeklickt wird. Das Eingabeschema erweitert sich entsprechend, die zusätzlichen Gleichungen werden eingetragen, und es kann wieder auf "Gleichungssystem lösen" geklickt werden:

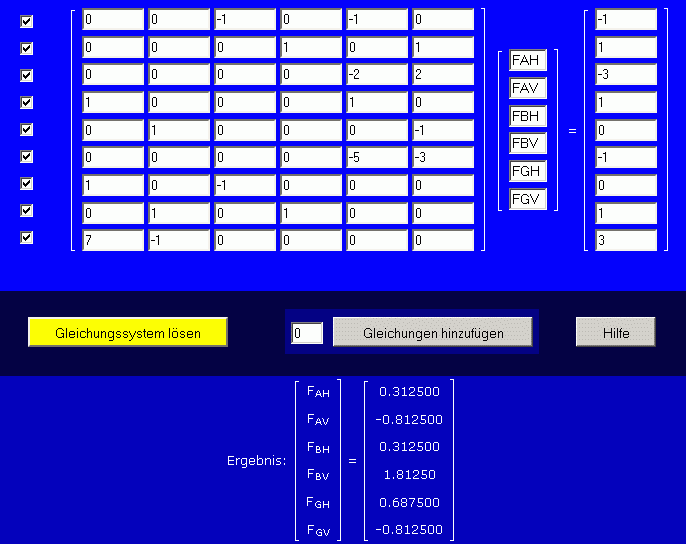
Wenn (wie hier) beide Rechnungen (mit 6 bzw. 9 Gleichungen) das gleiche Ergebnis liefern, dann ist dies ein sehr starkes Indiz für die Richtigkeit der Ergebnisse. Man kann noch weitere Rechnungen mit minimalem Aufwand durchführen, indem man das Häkchen vor einzelnen Gleichungen entfernt, die dann für eine folgende Rechnung nicht benutzt werden. Das Ergebnis darf sich nicht ändern.

Natürlich muss man hier sinnvolle Grenzen beachten: Es dürfen nicht mehr als 3 Gleichungen ausgesondert werden, und auch das Entfernen von 3 Gleichungen darf nicht beliebig erfolgen. Wenn man z. B. die Gleichungen 1, 4 und 7 unberücksichtigt lässt, dann meldet das Programm eine singuläre Koeffizientenmatrix, weil das mechanische System in Horizontalrichtung dann nicht mehr fixiert ist (die Gleichungen 1, 4 und 7 sind die Gleichgewichtsbedingungen für die Horizontalkräfte an den beiden Teilsystemen und am Gesamtsystem).

Es soll noch an einem Beispiel gezeigt werden, wie die Rechnung reagiert, wenn sich ein Fehler in die Gleichgewichtsbedingungen eingeschlichen hat. Nachfolgend ist nur ein Vorzeichen falsch, natürlich werden trotzdem Ergebnisse abgeliefert (die sind für das falsche Gleichungssystem die richtigen Ergebnisse):

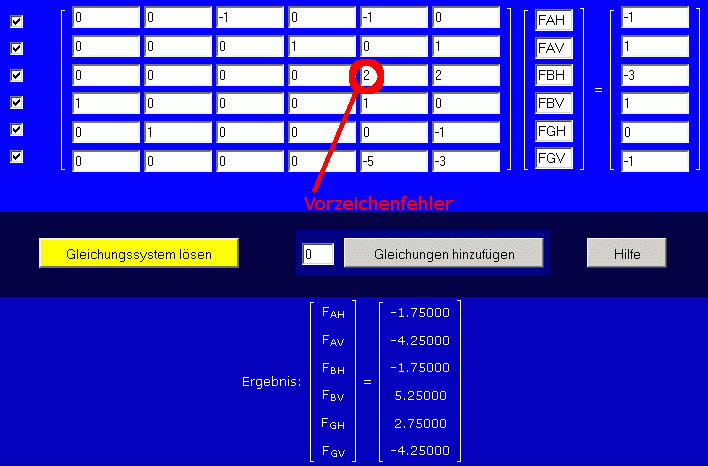
Der "kleine" Fehler führt zu völlig veränderten Ergebnissen und würde ohne Kontrollrechnung unbemerkt bleiben. Der gleiche Fehler bei einer Rechnung mit 9 Gleichungen wirkt sich folgendermaßen aus:

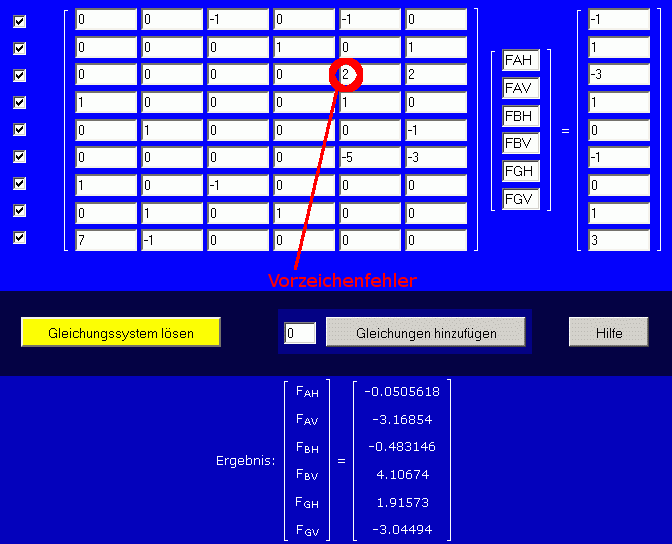
Auch bei dieser Rechnung wird natürlich ein Ergebnis abgeliefert (das richtige Ergebnis für das falsche System). Aber es es ein völlig anderes Ergebnis als bei der Rechnung mit 6 Gleichungen, und dieser Unterschied ist ein sicheres Indiz dafür, dass mindestens eine Gleichung des Systems falsch ist.