Lineares Gleichungssystem mit Bandmatrix

Lineares Gleichungssystem mit Bandmatrix

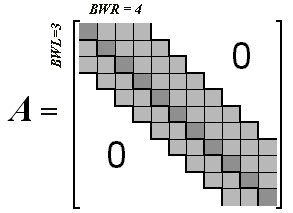
Beispiel einer Bandmatrix mit 11 Zeilen/Spalten, der linken Bandweite bwl=3 und der rechten Bandweite bwr=4
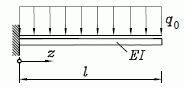
Beispiel 1: Für den skizzierten Träger mit konstanter Biegesteifigkeit EI ist die Durchbiegung näherungsweise mit dem Differenzenverfahren zu bestimmen.
Gegeben: a ; q0 ; EI = konstant .
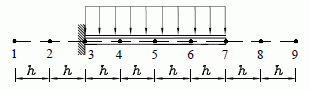
Im Kapitel "Computer-Verfahren für Biegeprobleme" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird gezeigt, dass sich bei der (sehr groben) Einteilung des Trägers in nur nA = 4 Abschnitte (nebenstehende Skizze) folgendes Gleichungssystem mit n = 9 unbekannten Vertikalverschiebungen v1, ... ,v9 (einschließlich der "Außenpunkte") ergibt:
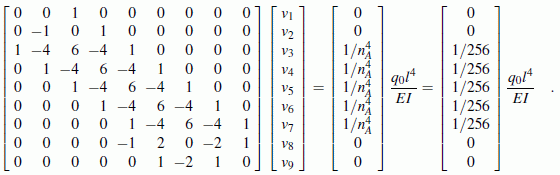
Die Koeffizientenmatrix ist bandförmig mit der linken Bandweite bwl = 4 und der rechten Bandweite bwr = 3 (die Bandweite zählt jeweils von dem Element, das von der Hauptdiagonalen am weitesten entfernt ist bis einschließlich Hauptdiagonalelement). Nach dem Start des Programms werden zunächst diese Werte eingestellt:
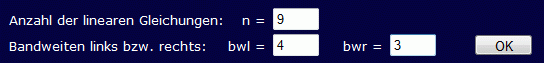
Nach Anklicken des OK-Buttons ändert sich das Eingabeschema entsprechend, und das Gleichungssystem kann eingegeben werden. Für Aufgaben dieser Art ist eine effektive Unterstützung vorgesehen. Nach Anklicken des Buttons "Automatischer Aufbau des Bandes" wird folgende Offerte unterbreitet:

Dieses Angebot entspricht exakt dem Aufbau der entsprechenden Gleichungen des behandelten Problems und kann mit Klick auf den Button "Werte übernehmen" angenommen werden. Im Eingabeschema füllen sich die Zeilen 3 bis 7. Nach Anklicken des Buttons "Automatischer Aufbau der rechten Seite" wird folgende Offerte unterbreitet:

Hier muss die 1 im Eingabefeld durch 1/256 ersetzt werden, danach kann der Button "Werte übernehmen" angeklickt werden. Nun müssen nur noch die Werte in den beiden ersten und den beiden letzten Zeilen der Matrix im Eingabeschema "von Hand" eingetragen werden. Das komplett ausgefüllte Eingabeschema sollte schließlich so aussehen:
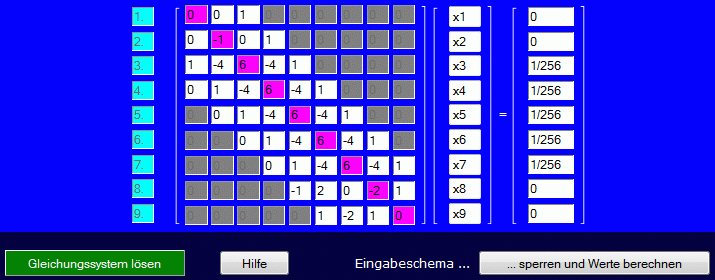
Dass hier auch noch die Namen der Unbekannten auf v1, ... ,v9 geändert wurden (Voreinstellung ist x1, ... ,x9), ist natürlich nicht erforderlich. Nach Anklicken von "Gleichungssystem lösen" erscheint das Ergebnis:

Das Angebot, die Rechnung mit einer geänderten Anzahl von Gleichungen zu wiederholen, ist mit minimalem Aufwand zu realisieren. Das sollte allerdings schon beim Start der ersten Rechnung bedacht werden. Man findet die Beschreibung dieses Beispiels mit der Realisierung der Wiederholung der Rechnung mit feinerer Diskretisierung auf der Seite "Einstiegsbeispiel zum Differenzenverfahren mit TM-interaktiv".
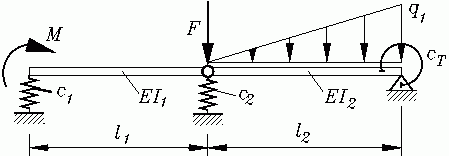
Beispiel 2: Für den skizzierten Träger soll die Durchbiegung näherungsweise mit dem Differenzenverfahren berechnet werden.
Gegeben:
l1 = 1200 mm ;
EI1 = 2,5 kNm2 ;
c1 = 50 N/mm ;
l2 = 1300 mm ;
EI2 = 5 kNm2 ;
c2 = 250 N/mm ;
cT = 5 kNm ;
q1 = 1,3 N/mm ;
F = 800 N ;
M = 250 Nm .
Im Kapitel "Computer-Verfahren für Biegeprobleme" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird diese Aufgabe ausführlich behandelt. Hier findet man die detailliert kommentierte Lösung mit dem Programm "Lineares Gleichungssystem mit Bandmatrix".
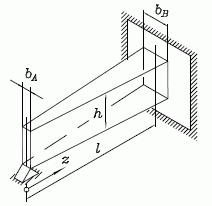
Beispiel 3: Der skizzierte Träger mit Rechteckquerschnitt (konstante Höhe, linear veränderliche Breite) ist nur durch sein Eigengewicht belastet.
![]()
Mit dem Differenzenverfahren ist näherungsweise die Durchbiegung bei Annahme eines Breitenverhältnisses λ = 2 zu berechnen.
Das besondere Problem beim Aufbau des Gleichungssystems für diese Aufgabe ist, dass für jede Gleichung eine andere Belastungsintensität und eine andere Biegesteifigkeit zu berücksichtigen sind. Beim automatischen Aufbau der Gleichungen kann dafür die Variable z_nr benutzt werden, die automatisch verfügbar ist und die jeweilige Zeilennummer der aktuellen Gleichung enthält.
Aufbau und Lösung des Gleichungssystems werden ausführlich beschrieben auf der Seite Differenzenverfahren, Biegeträger mit veränderlichem Querschnitt, Lösung mit TM-interaktiv. Es werden Gleichungssysteme mit 105 bis 5005 Gleichungen berechnet.
