Beispiel zum Programm Anfangswertproblem

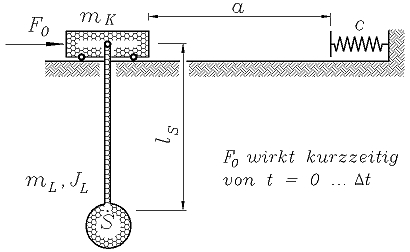
Eine Laufkatze (Masse m_K) trägt eine Last (Masse einschließlich Anhängevorrichtung: m_L, Massenträgheitsmoment bezüglich des Schwerpunktes S: J_L). In der skizzierten Ruhelage beginnt für eine kurze Zeit Δt die konstante Antriebskraft F₀ zu wirken, die danach wieder abgeschaltet wird. Nach dem Zurücklegen der Strecke a stößt die Laufkatze auf einen elastischen Puffer (Federzahl c).

Die Bewegung von Laufkatze und Last soll, beginnend aus der Ruhelage, für die ersten 10 Sekunden analysiert werden.

Gegeben:

m_K = 100 kg ;  J_L = 400 kgm² ;  l_S = 4 m ;  F₀ = 2000 N ;
m_L = 500 kg ;  c = 200000 N/m ;  Δt = 1 s ;  a = 5 m .

Die Aufgabe wird im Lehrbuch "Dankert/Dankert: Technische Mechanik" in den Kapiteln "Prinzipien der Mechanik" (Aufschreiben der Bewegungs-Differenzialgleichungen) und "Verifizieren von Computerrechnungen" (Diskussion der Ergebnisse) behandelt.

Die Besonderheit dieser Aufgabe besteht in dem Eintreten von unterschiedlichen "Ereignissen" (Abschalten der Antriebskraft, Zu- und Abschalten einer Feder). Man erfasst sie, indem an die Stelle der Kraft F₀ die zeitabhängige Kraft F_t tritt und die Federkonstante c durch c_t ersetzt wird:

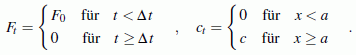
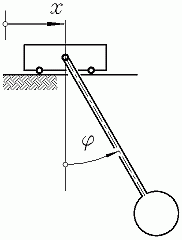
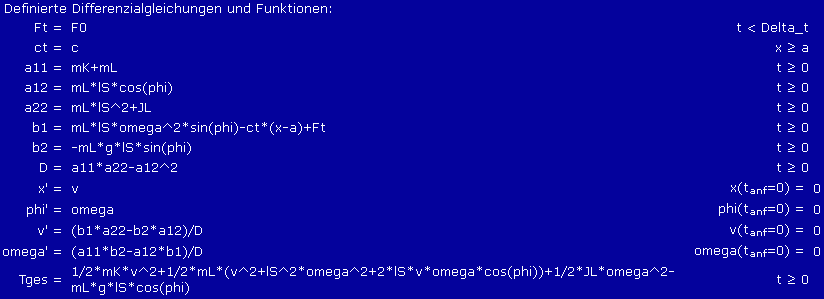
Unter Verwendung der nebenstehend skizzierten Koordinaten gelten folgende Bewegungs-Differenzialgleichungen (die ausführlich kommentierte Herleitung findet man im Kapitel "Prinzipien der Mechanik"):

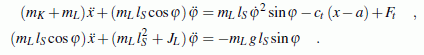
Dieses Differenzialgleichungssystem hat aus mathematischer Sicht alle denkbaren unangenehmen Eigenschaften: Es ist hochgradig nichtlinear, in den Beschleunigungsgliedern gekoppelt, und es sind ein zeitabhängiges und ein wegabhängiges Ereignis zu berücksichtigen. Die Lösung kann nur numerisch gelingen.

Das Programm "Anfangswertproblem" erwartet ein Differenzialgleichungssystem 1. Ordnung. Deshalb werden die beiden neuen Variablen v und ω eingeführt:

Damit kann das Anfangswertproblem so formuliert werden, wie man es (fast) dem Programm "Anfangswertproblem" anbieten kann:

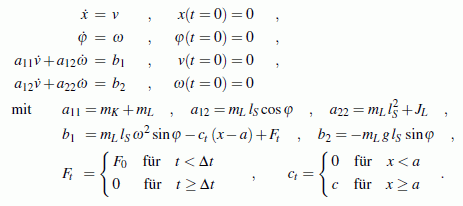
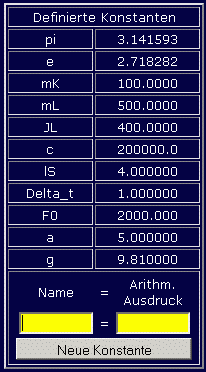
Bleibt nur noch das Problem, dass das Programm "Anfangswertproblem" die nach den ersten Ableitungen aufgelösten Differenzialgleichungen erwartet. Die 3. und 4. Differenzialgleichung bilden ein einfaches lineares Gleichungssystem, dessen Lösung man zum Beispiel sofort nach der Cramerschen Regel aufschreiben kann, so dass man schließlich diese vier Differenzialgleichungen hat:

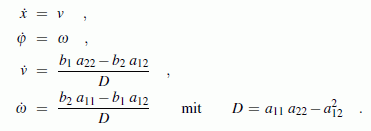
Nach dem Start des Programms "Anfangswertproblem" werden zunächst die gegebenen Parameter als Konstanten definiert, zusätzlich die Erdbeschleunigung g. Rechts sieht man die Tabelle mit den beiden vordefinierten Konstanten pi und e und den zusätzlich definierten Parametern mK, mL, JL, c, lS, Delta_t, F0, a und g, alle mit den zueinander passenden Dimensionen N, kg, m, s.

Die Voreinstellungen für den Integrationsbereich (t_anf, t_end, n_steps) werden nicht verändert, obwohl zu vermuten ist, dass die voreingestellte Anzahl der Integrationsschritte n_steps = 500 für die komplizierte Bewegung nicht genügen wird. Aber man muss ohnehin mehrfach rechnen. Zunächst werden die Funktionen, mit denen die Differenzialgleichungen beschrieben werden, eingegeben, zum Beispiel:

Zu jeder Funktion gehört ein Gültigkeitsbereich. Hier wurde x ≥ a eingegeben. Das bedeutet, dass ct für x < a den Wert 0 hat. Im Eingabeprotokoll unter der Eingabezeile sieht man die vorab eingegebene Funktion Ft mit ihrem Gültigkeitsbereich. Bei der Eingabe einer Differenzialgleichung (vom Programm wird dies daran erkannt, dass im Eingabefeld "Name" der Funktionsname jeweils mit dem Zeichen ' ergänzt werden muss) wird die zugehörige Anfangsbedingung abgefordert. Das sieht zum Beispiel so aus:

Die Eingaben werden unterhalb des Eingabebereichs protokolliert. Wenn alle Funktionen und Differenzialgleichungen eingegeben sind, sollte vor der Berechnung immer das Angebot "Syntaxcheck" genutzt werden. Nach Anklicken des entsprechenden Buttons sieht das Eingabeprotokoll so aus:

Nun kann der Button "Berechnung starten" angeklickt werden. Als Ergebnisse erscheinen zunächst die Zahlenwerte am Ende des Berechnungsintervalls für die vier Funktionen, die als Lösungen der vier Differenzialgleichungen ermittelt wurden, und die grafische Darstellung dieser Funktionen über das gesamte Berechnungsintervall in einem Diagramm:

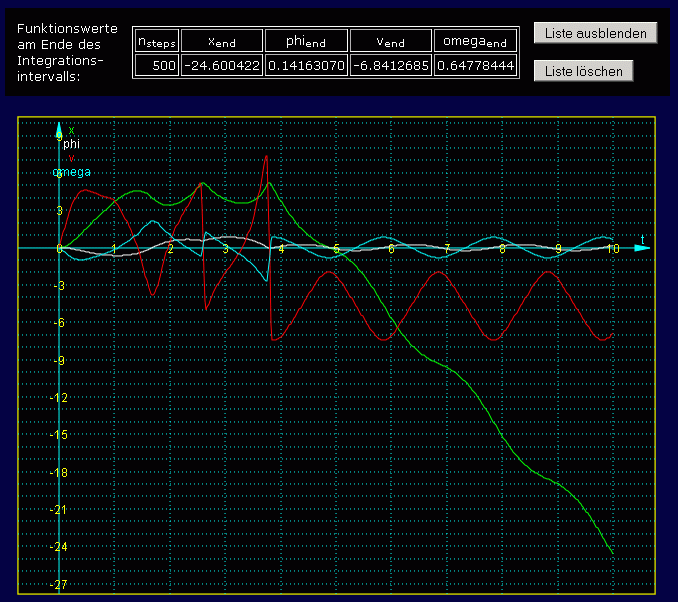
Das ist natürlich etwas unübersichtlich und wird nachfolgend noch verbessert. Zunächst aber muss überprüft werden, ob man den Ergebnissen vertrauen kann. Man sollte grundsätzlich mindestens eine zweite Rechnung mit einer größeren Schrittanzahl durchführen und die Endwerte vergleichen, die im Programm gesammelt werden. Nachfolgend sieht man die Werte am Ende des Berechnungsintervalls für insgesamt 5 Rechnungen mit unterschiedlicher Schrittanzahl:

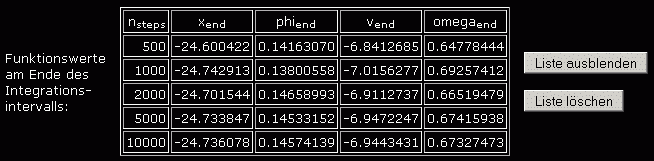
Die Werte dieser Rechnungen weichen nur unbedeutend voneinander ab, so dass man ihnen vertrauen kann (und ab n_steps = 5000 genügen sie sogar gehobenen Genauigkeitsansprüchen). Trotzdem soll noch eine zusätzliche Kontrolle realisiert werden, die bei diesem System recht anschaulich ist.

Es bietet sich an, die Energiekurve als Kontrollfunktion parallel zur numerischen Integration der Bewegungs-Differenzialgleichungen zu ermitteln. Die potenzielle Energie soll nur für das bewegte System berücksichtigt werden (während des Kontakts mit der Feder ist auch in dieser potenzielle Energie gespeichert). Im oben genannten Lehrbuch wird gezeigt, dass mit dem Null-Potenzial entsprechend nebenstehender Skizze und den Anteilen der kinetischen Energie aus der Bewegung von Laufkatze und pendelnder Last folgende Beziehung für die Gesamtenergie des bewegten Systems gilt:

Diese Funktion wird zusätzlich eingegeben. Das erweiterte Eingabeprotokoll sieht dann so aus:

Nach erneutem Anklicken des Buttons "Berechnung starten" ändert sich an der Ergebnisanzeige zunächst nichts. Die Werte für die zusätzliche Funktion werden zwar berechnet, automatisch angezeigt werden aber nur Ergebnisse der Integration der Differenzialgleichungen. Zur individuellen Einstellung der grafischen Darstellung steht unterhalb der Grafik ein blaues Feld zur Verfügung, in dem die gewünschten Parameter eingestellt werden können. Zuächst wird die Anzahl der Grafikfenster (Standardeinstellung: 1) auf 4 erhöht (1, 2 oder 4 sind möglich). Das blaue Feld erweitert sich entsprechend, folgende Änderungen werden vorgenommen: In den Grafikfenstern 1 und 2 (oben) soll nur die besonders interessante Bewegungskoordinate x der Laufkatze dargestellt werden, was jeweils durch entsprechende Änderung im Eingabefeld "Funktionen" realisiert wird. Im Graphikfenster 2 wird der Darstellungsbereich so geändert, dass die interessante Phase des Anschlags an die Feder deutlich wird. Im Graphikfenster 3 (links unten) wird die Bewegung der pendelnden Last (Koordinate phi) dargestellt. Im Grafikfenster 4 schließlich soll Tges dargestellt werden. Nachdem auch noch einige sinnvolle Änderungen für die Raster der einzelnen Fenster vorgenommen wurden, sieht das blaue Feld zum Beispiel so aus:

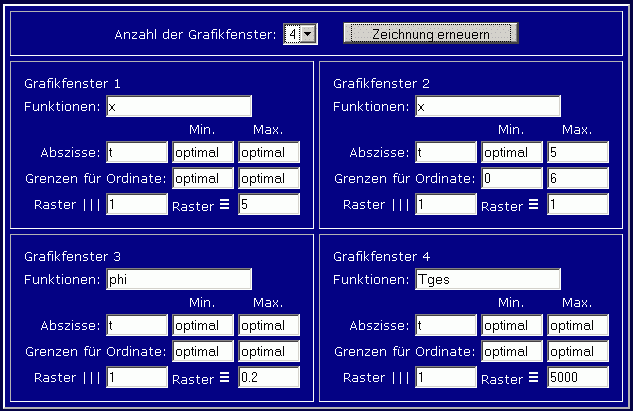
Nach Anklicken des Buttons "Zeichnung erneuern" sieht die Grafik so aus:

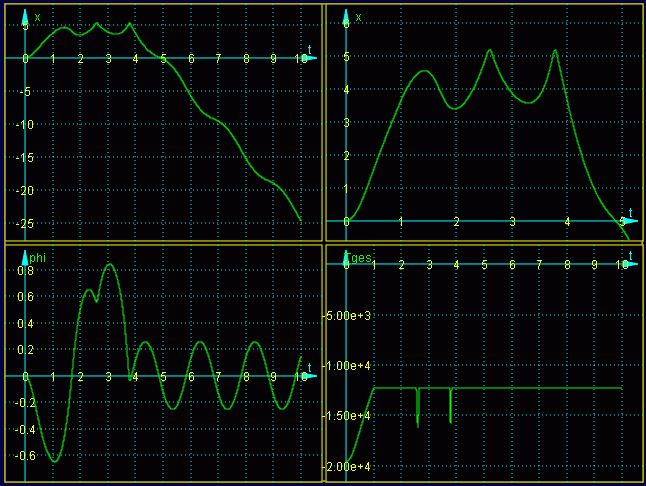
Interessant ist die Bewegung der Laufkatze (Fenster oben rechts): Bevor sie ihren Rückweg antritt, gibt es insgesamt fünfmal eine Umkehr der Bewegungsrichtung, erstmals kurz nach dem Abschalten der Antriebskraft deutlich vor dem Erreichen der Feder. Es folgt aber unmittelbar eine weitere Umkehr (wie die erste ohne äußere Krafteinwirkung), so dass es doch zum Anschlag an die Feder kommt. Nach dem (ersten) Kontakt mit der Feder gibt es eine weitere (die dritte) Umkehr der Bewegungsrichtung ohne äußere Krafteinwirkung, so dass es zu einem zweiten Anschlag an die Feder kommt, der dann eine recht gleichmäßig verlaufende Bewegung (Rückweg) einleitet. Hier kann man eine Animation der Bewegung sehen.

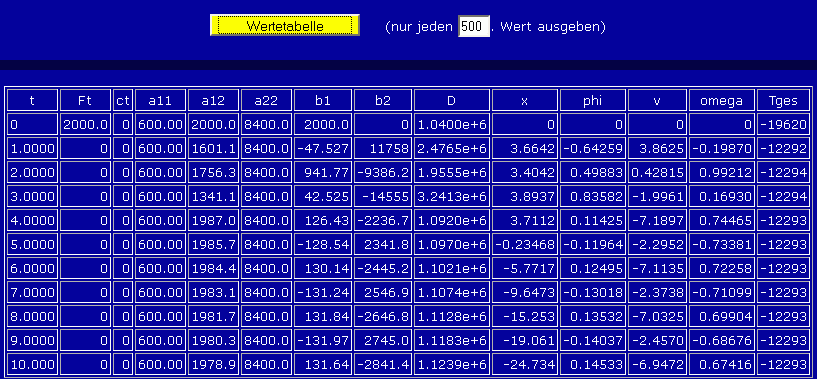
Die Kontrollfunktion startet mit dem Wert für die potenzielle Energie der Last im Ruhezustand T_ges(t=0) = − m_L g l_S = − 19620 Nm. Die Arbeit der konstanten Kraft F₀ auf dem Weg von x = 0 … x₁ = x(t = 1 s) erhöht die Energie im bewegten System um F₀ x₁. Die beiden "Zacken" in der Energiekurve kennzeichnen die vorübergehende Abgabe von Energie an die Feder, die aber jeweils zurückgegeben wird. Man findet die Zahlenwerte bestätigt, wenn man sich die Wertetabelle (Klick auf den gelben Button) listen lässt (Vorsicht, vorher die Einstellung anpassen, damit nicht alle Werte ausgegeben werden):