Anfangswertproblem
Anfangswertproblem
Beispiel: Eine Funktion Ft = F mit dem Gültigkeitsbereich t ≤ Dt hat in diesem Bereich den Wert F, für t > Dt den Wert 0.
Wenn ein Name eingegeben wird, dem das Zeichen ' folgt (siehe Beispiel links),
wird die Definition einer Differenzialgleichung vermutet, und der Eingabebereich
(siehe oben rechts) wird für die Eingabe der zugehörigen
Anfangsbedingung vorbereitet. Der mit 0 vorbelegte Wert kann auch durch
einen arithmetischen Ausdruck verändert werden.
Wegweiser zu den Beispielen:
- Beispiel 1 behandelt ein einfaches Stabpendel mit großen Ausschlägen (System mit einem Freiheitsgrad). Diese Aufgabe ist das Standard-Demonstrationsbeispiel im Skript "Numerische Integration von Anfangswertproblemen, Teil 1" (PDF, 39 Seiten), in dem die verschiedenen Integrationsverfahren vorgestellt und verglichen werden. Hier ist es das einfache Einführungsbeispiel in das Arbeiten mit dem Programm "Anfangswertproblem".
- Beispiel 2 ist ein System mit einem Freiheitsgrad, bei die Umkehr der Reibkraftrichtung bei Umkehr der Bewegungsrichtung mit Hilfe des Gültigkeitsbereichs von Funktionen realisiert wird.
- Beispiel 3 ist ein System mit zwei Freiheitsgraden, bei dem ein zeitabhängiges Ereignis zu berücksichtigen ist (Funktion, die zu einem vorbestimmten Zeitpunkt ihren Verlauf ändert).
- Beispiel 4 ist ein System mit zwei Freiheitsgraden, bei dem die Differenzialgleichungen in den Beschleunigungsgliedern gekoppelt sind.
- Beispiel 5 ist ein System mit zwei Freiheitsgraden, bei dem Differenzialgleichungen in den Beschleunigungsgliedern gekoppelt sind und außerdem ein zeitabhängiges und mehrere wegabhängige Ereignisse zu berücksichtigen sind.
- Beispiel 6 ist ein System mit einem Freiheitsgrad, bei dem nur die Winkelgeschwindigkeit gesucht ist, die dann für die Auswertung einer Funktion benutzt wird.
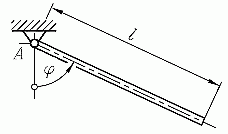Beispiel 1: Ein dünner Stab der
Länge l mit konstantem
Querschnitt ist an einem Ende reibungsfrei gelagert. Er
wird aus der vertikalen Lage um den Winkel
φ0 ausgelenkt
und ohne Anfangsgeschwindigkeit freigegeben (Luftwiderstand kann
vernachlässigt werden).
Gegeben: l = 1 m ; Erdbeschleunigung g = 9,81 m/s2 , φ0 = 3π/4.
Es sind die Bewegungsgesetze φ(t) und ω(t) für die ersten 10 Sekunden der Bewegung zu ermitteln.
Im Kapitel 29 des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird das Anfangswertproblem für diese Aufgabe hergeleitet:
Dieses Anfangswertproblem 2. Ordnung kann durch Einführen einer neue Variablen ω für die erste Ableitung von φ in ein Anfangswertproblem 1. Ordnung überführt werden, das in dieser Form dem Programm "Anfangswertproblem" angeboten werden kann. Hier findet man die ausführliche Beschreibung der kompletten Rechnung, die schließlich folgendes Ergebnis hat:
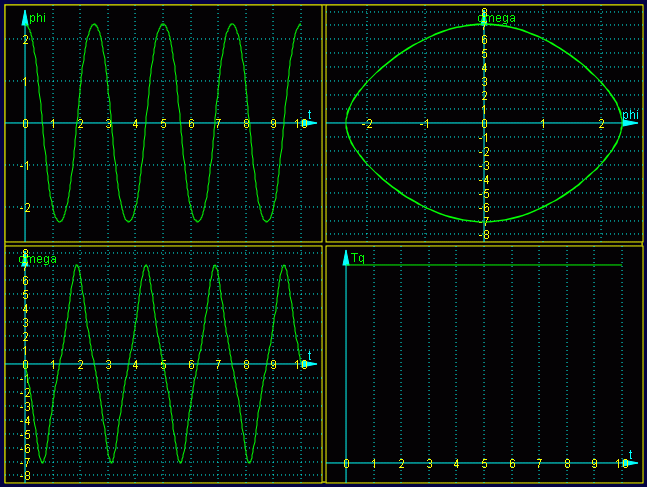
φ(t) (links oben), ω(t) (links unten) ω(φ) (rechts oben) und
als Kontrollfunktion (rechts unten) die Gesamtenergie
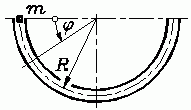Beispiel 2: Ein Massenpunkt
m wird wie skizziert in eine halbkreisförmige
Rinne gelegt und ohne Anfangsgeschwindigkeit freigegeben. Das
Bewegungsgesetz φ(t) soll
bei Berücksichtigung der Gleitreibung
zwischen Massenpunkt und Rinne für die ersten
10 Sekunden der Bewegung berechnet werden.
Gegeben: R = 1 m ; Erdbeschleunigung g = 9,81 m/s2 ; μ =0,05 .
Im Kapitel 28 des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird das Anfangswertproblem für diese Aufgabe hergeleitet:
Das Problem steckt im zweiten Term der Differenzialgleichung: Weil bei Umkehr der Bewegungsrichtung die Reibkraft auch ihre Richtung ändert, wurde die Signum-Funktion verwendet (mit der Winkelgeschwindigkeit als Argument). Wie dies mit dem Programm "Anfangswertproblem" realisiert werden kann, wird hier ausführlich beschrieben. Die Berechnung führt schließlich auf folgendes Ergebnis:
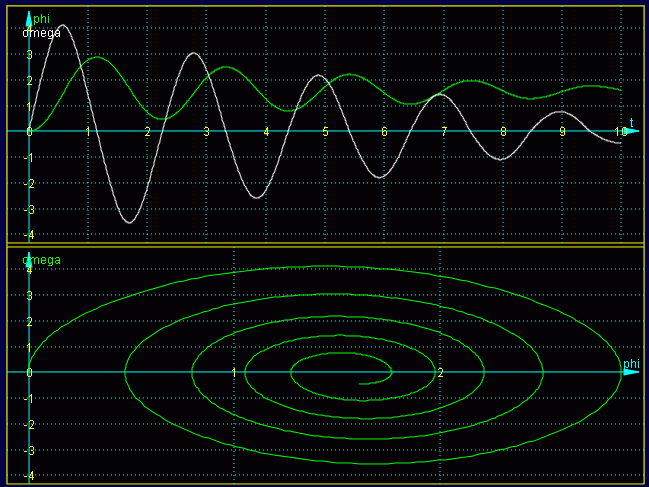
φ(t) und ω(t) (oben), ω(φ) (unten)
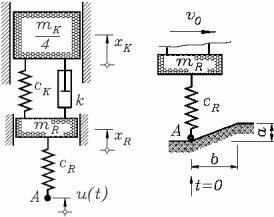Beispiel 3: Für die Analyse der Vertikalschwingungen
eines Rades infolge der Bodenunebenheiten
und der Übertragung der Schwingungen auf
die Karosse dient das skizzierte Berechnungsmodell: Zwischen dem Rad (Masse
mR)
und der Karosserie befinden sich eine Feder und ein Dämpfungsglied
(Stoßdämpfer mit geschwindigkeitsproportionaler
Dämpfung), auf denen näherungsweise ein Viertel der
Karosseriemasse mK lastet. Die
Elastizität der Bereifung wird durch die Federzahl
cR erfasst. Dem Punkt
A wird die Vertikalbewegung
u(t) aufgezwungen.
| Gegeben: | mK = | 1000 kg ; | cK = | 300 N/cm ; | k = | 750 kg/s ; | v0 = | 50 km/h ; |
| mR = | 25 kg ; | cR = | 900 N/cm ; | a = | 20 cm ; | b = | 40 cm . |
Es sollen die Vertikalschwingungen des Rades und der Karosserie ermittelt werden (Analyse der Bewegungen für 0 ≤ t ≤ 3 s), wenn der Punkt A zum Zeitpunkt t = 0 eine Aufwärtsbewegung auf einer geneigten Linie (rechte Skizze) beginnt und nach Erreichen der Höhe a sich horizontal weiter bewegt. Es soll angenommen werden, dass bis zum Erreichen der Höhe a eine horizontale Strecke b mit einer konstanten Geschwindigkeit v0 zurückgelegt wird, so das der Punkt A diese Strecke nach Δt = b/v0 zurückgelegt hat.
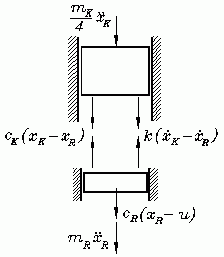
Die nebenstehende Schnittskizze gestattet die Formulierung der Bewegungs-Differenzialgleichungen (zum Beispiel mit Hilfe des Prinzips von d'Alembert):
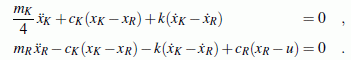
Sämtliche Anfangswerte (beide Koordinaten und ihre Ableitungen) haben den Wert 0. Das lineare Differenzialgleichungssystem kann mit erträglichem Aufwand nur numerisch gelöst werden, weil die Funktion u(t) das Problem erheblich erschwert. Für diese Funktion gilt:
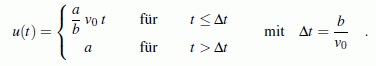
Hier findet man die ausführliche Beschreibung der kompletten Rechnung mit dem Programm "Anfangswertproblem", die auf folgendes Ergebnis führt:
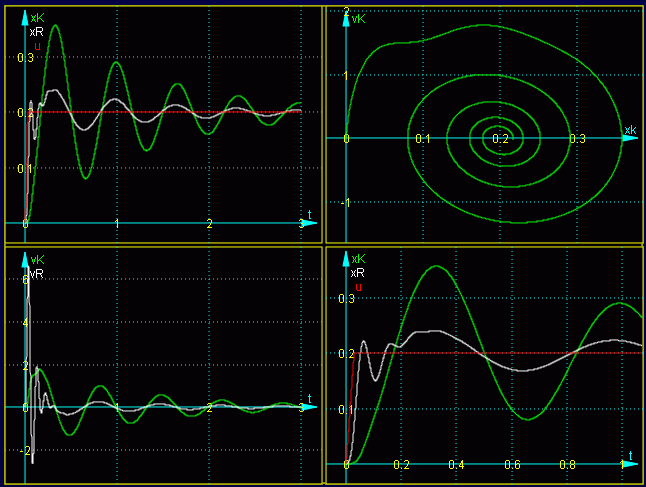
xK(t), xR(t) und u(t) (links oben und rechts unten),
Geschwindigkeiten vK(t) und vR(t) (links unten) und vK(xK) (rechts oben)
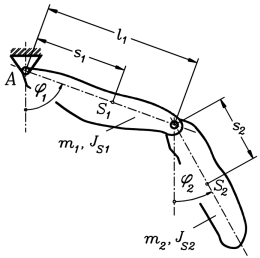
Beispiel 4: Ein Doppelpendel wird definiert durch die beiden Pendelmassen m1 und m2, die auf die jeweiligen Schwerpunkte bezogenen Massenträgheitsmomente JS1 und JS2, die Schwerpunktabstände von den Drehpunkten s1 und s2 und den Abstand l1 der beiden Drehpunkte voneinander.
Die Bewegung soll durch die Funktionen φ1(t) und φ2(t) beschrieben werden, die für das Zeitintervall t = 0 ... 10 s zu berechnen sind.
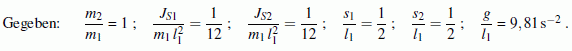
Die Aufgabe wird im Lehrbuch "Dankert/Dankert: Technische Mechanik" in den Kapiteln "Prinzipien der Mechanik" (Aufschreiben der Bewegungs-Differenzialgleichungen) und "Verifizieren von Computerrechnungen" (Diskussion der Ergebnisse) behandelt.
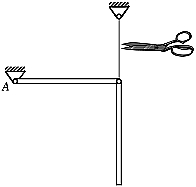
Die gegebenen Werte gelten für zwei schlanke Stäbe gleicher Masse und gleicher Länge. Sie sollen aus der nebenstehend skizzierten Anfangslage ohne Anfangsgeschwindigkeiten freigelassen werden, so dass folgende Anfangsbedingungen gelten:
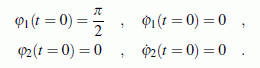
Im oben genannten Lehrbuch wird die (nicht ganz einfache) Herleitung der Bewegungs-Differenzialgleichungen ausführlich beschrieben. Unter Verwendung der in der Aufgabenstellung skizzierten Koordinaten erhält man:
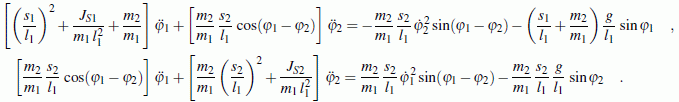
Die Differenzialgleichungen sind in den Beschleunigungsgliedern (2. Ableitungen der Winkelkoordinaten) gekoppelt. Hier findet man die Aufbereitung des Problems unter diesem speziellen Gesichtspunkt und die komplette Rechnung mit dem Programm "Anfangswertproblem", die auf folgendes Ergebnis führt:
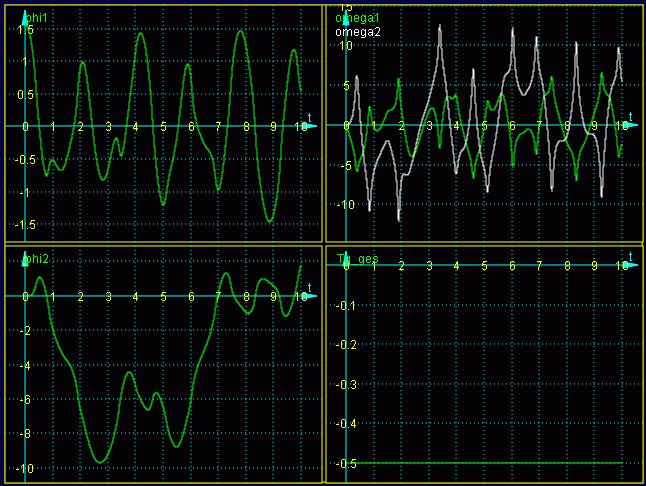
φ1(t) (links oben), φ2(t) (links unten), Winkelgeschwindigkeiten ω1(t) und ω2(t) (rechts oben)
und als Kontrollfunktion (rechts unten) die Gesamtenergie
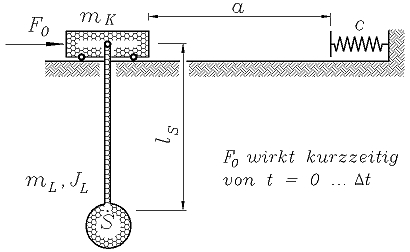
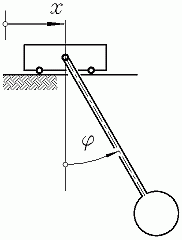
Beispiel 5: Eine Laufkatze (Masse mK) trägt eine Last (Masse einschließlich Anhängevorrichtung: mL, Massenträgheitsmoment bezüglich des Schwerpunktes S: JL). In der skizzierten Ruhelage beginnt für eine kurze Zeit Δt die konstante Antriebskraft F0 zu wirken, die danach wieder abgeschaltet wird. Nach dem Zurücklegen der Strecke a stößt die Laufkatze auf einen elastischen Puffer (Federzahl c).
Die Bewegung von Laufkatze und Last soll, beginnend aus der Ruhelage, für die ersten 10 Sekunden analysiert werden.
Gegeben:
mK = 100 kg ; JL = 400 kgm2 ; lS = 4 m ; F0 = 2000 N ;
mL = 500 kg ; c = 200000 N/m ; Δt = 1 s ; a = 5 m .
Die Aufgabe wird im Lehrbuch "Dankert/Dankert: Technische Mechanik" in den Kapiteln "Prinzipien der Mechanik" (Aufschreiben der Bewegungs-Differenzialgleichungen) und "Verifizieren von Computerrechnungen" (Diskussion der Ergebnisse) behandelt.
Die Besonderheit dieser Aufgabe besteht in dem Eintreten von unterschiedlichen "Ereignissen" (Abschalten der Antriebskraft, Zu- und Abschalten einer Feder). Man erfasst sie, indem an die Stelle der Kraft F0 die zeitabhängige Kraft Ft tritt und die Federkonstante c durch ct ersetzt wird:
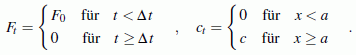
Unter Verwendung der nebenstehend skizzierten Koordinaten gelten folgende Bewegungs-Differenzialgleichungen (die ausführlich kommentierte Herleitung findet man im Kapitel "Prinzipien der Mechanik"):
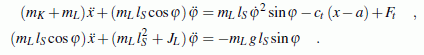
Dieses Differenzialgleichungssystem hat aus mathematischer Sicht alle denkbaren unangenehmen Eigenschaften: Es ist hochgradig nichtlinear, in den Beschleunigungsgliedern gekoppelt, und es sind ein zeitabhängiges und ein wegabhängiges Ereignis zu berücksichtigen. Die Lösung kann nur numerisch gelingen.
Hier findet man die Aufbereitung des Problems und die komplette Rechnung mit dem Programm "Anfangswertproblem", die auf folgendes Ergebnis führt:
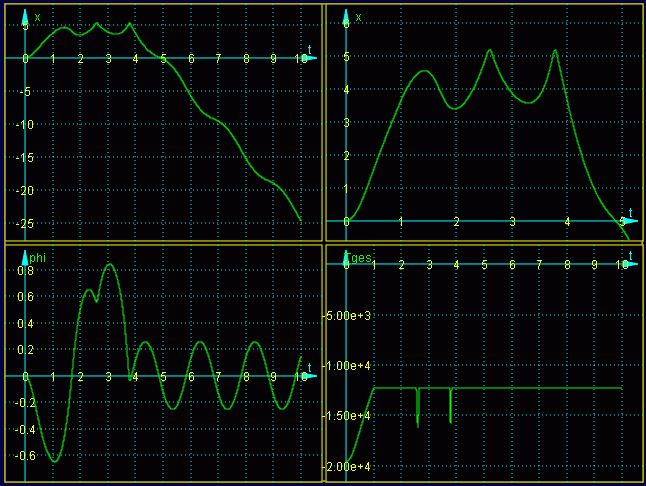
x(t) (oben links und rechts), φ(t) (links unten) und als Kontrollfunktion (rechts unten) die Gesamtenergie
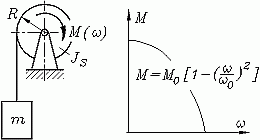Beispiel 6: Eine Seilwinde wird von einem Antrieb mit "fallender Kennlinie"
(Antriebsmoment wird bei größerer Drehzahl kleiner) angetrieben. Aus der
Ruhe heraus wird eine Masse m angehoben
(das Seil sei dehnstarr und
masselos).
Für den Anfahrvorgang sollen die Winkelgeschwindigkeit der Winde und das Antriebsmoment in Abhängigkeit von der Zeit ermittelt werden.
Gegeben:
Im Kapitel "Ebene Bewegung starrer Körper des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird das Anfangswertproblem für diese Aufgabe hergeleitet:
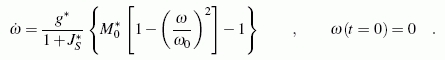
Wie dies interaktiv mit dem Programm "Anfangswertproblem" realisiert werden kann, wird hier ausführlich beschrieben. Die Berechnung führt schließlich auf folgendes Ergebnis:
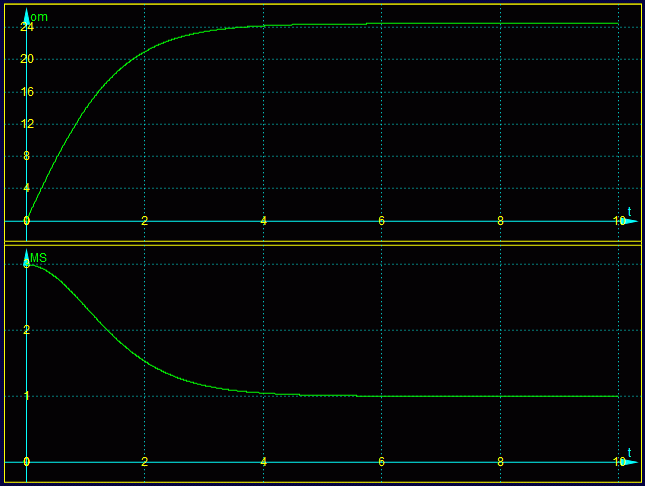
ω(t) (oben), M *(t) = M/(mgR)(t) (unten)
