Allgemeines ebenes Kraftsystem

Wegweiser zu den Beispielen
- Beispiel 1: Berechnung der Resultierenden von 4 Einzelkräften,
- Beispiel 2: Gleichgewicht herstellen mit 3 Kräften,
- Beispiel 3: Gleichgewicht herstellen mit 2 Kräften (Eingabe mit einem arithmetischen Ausdruck),
- Beispiel 4: Gleichgewicht herstellen mit Kraft und Doppelkraft (Seilkraft, die in gleicher Größe zweimal am starren Körper angreift),
- Beispiel 5: Gleichgewicht herstellen mit 3 Kräften (als Belastung wirken u. a. Einzelmomente).
Beispiel 1: An einem starren Körper greifen wie skizziert vier Kräfte an. Man ermittle die Resultierende und die Lage und Richtung ihrer Wirkungslinie (Aufgabe entnommen aus dem Kapitel "Das allgemeine ebene Kraftsystem" des Lehrbuchs "Dankert/Dankert: Technische Mechanik").
Gegeben: F1 = 1 kN ; F2 = 2 kN ; F3 = 2 kN ; F4 = 1,5 kN ; α = 45° ; β = 60° ; a = 2 m .Um eine bessere Orientierung bei der Positionierung der Kräfte zu haben, empfiehlt es sich, nach Klick auf "Polygon erzeugen" (rechts unten in der Button-Leiste) ein Rechteck zu zeichnen (durch Klicken der Eckpunkte und abschließen mit Klick auf "Polygon schließen"):
Danach werden die Kräfte eingegeben, wobei man die Wahl zwischen "Betrag und Richtung" bzw. "Zwei Komponenten" hat. Nach Eingabe von F1 mit dem Betrag 1 und dem Winkel 0° wird "Kraft und Winkel eingeben" angeklickt, und die Kraft erscheint in der Grafik mit zwei farbig gekennzeichneten Punkten:
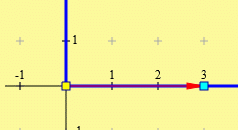
Mit Hilfe dieser Punkte kann die Kraft in der Ebene platziert werden (was man sich für die Kraft F1 natürlich ersparen könnte). Man kann die gewünschten Koordinaten für einen der beiden Punkte in die dafür vorgesehenen Eingabefelder eintragen oder einen der beiden Punkte in der Grafik mit der Maus verschieben. Durch Klicken auf "Punkt fixieren" ist die Kraft in ihrer endgültigen Position angekommen. Hier wurde der hellblaue Punkt mit der Maus in den Nullpunkt des Koordinatensystems verschoben, danach wird nur für diesen Punkt das Fixieren angeboten:

Bei der Eingabe der Kraft F2 mit dem Betrag 2 muss der Winkel α2 = −45° (negativ entsprechend der Definition über positive Winkel) eingegeben werden, nach Eingabe der Kraft F3 mit dem Betrag 2 und dem Winkel α3 = 60° sieht die Zeichenfläche nach Klicken auf "Kraft und Winkel eingeben" so aus:
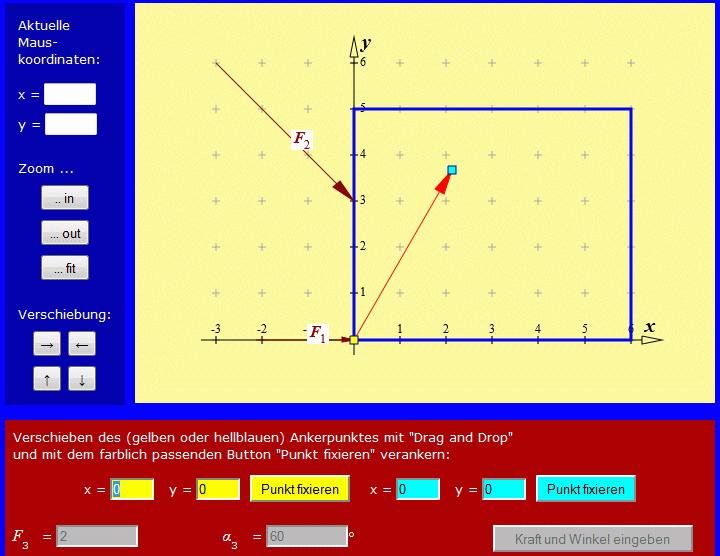
Wieder hat man die Wahl, die Koordinaten für den gelben bzw. hellblauen Punkt einzugeben oder aber den gelben Punkt mit der Maus in der Zeichenfläche zu verschieben. Wenn man die Mauseingabe wählt, passen sich die Eingabe-Buttons entsprechend an:
![]()
Nach Eingabe der Kraft F4 (entweder als F4 = 1.5 mit α4 = −90° oder über die Zeile darunter als F4x = 0 und F4y = −1.5) ist die Eingabe komplett. Nach Anklicken von "Resultierende berechnen" sollte die Grafik so aussehen:
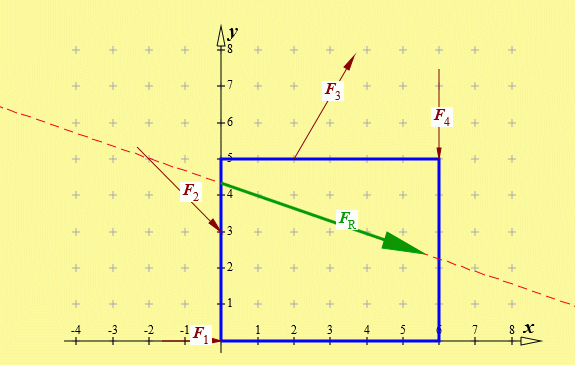
Die eingegebenen Kräfte werden immer unmittelbar nach einer Eingabe protokolliert, am Ende wird dieser Bereich mit den errechneten Ergebnissen komplettiert:
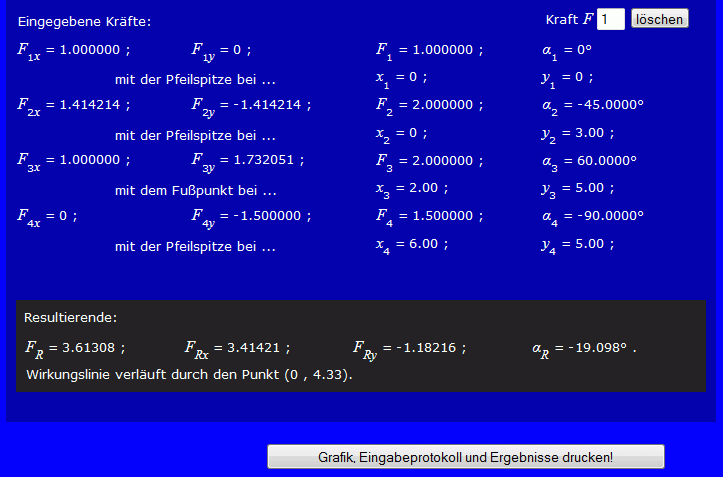
Wenn man das Angebot "Grafik, Eingabeprotokoll und Ergebnisse drucken" annimmt, werden die wichtigsten Informationen zusammengestellt und zum Drucker geschickt. Hier kann man sich die Variante ansehen, die beim Druck mit einem (als Freeware verfügbaren) "PDF-Treiber" entsteht.
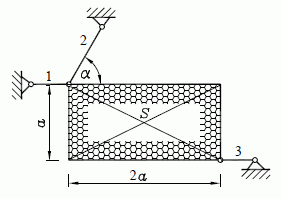
Beispiel 2: (Aufgabe entnommen aus dem Kapitel "Gleichgewicht des ebenen Kraftsystems" des Lehrbuchs "Dankert/Dankert: Technische Mechanik") Eine rechteckige Scheibe (Gewichtskraft FG) ist wie skizziert an drei Seilen aufgehängt.
Gegeben: FG = 2 kN ; α = 60° .Man ermittle die Kräfte in den Seilen 1 bis 3.
Für die Länge a wird (willkürlich) der Wert 1 angenommen, zur Orientierung (erforderlich ist das nicht) wird ein Rechteck gezeichnet und "Zoom ... fit" angeklickt. Die Kraft FG = 2 wird entweder als F1 = 2 und α1 = -90° und Klick auf "Kraft und Winkel eingeben" definiert oder aber über F1x = 0 und F1y = -2 und Klick auf "Kraftkomponenten eingeben". Nachdem man den (gelben) Fußpunkt der Kraft in die Mitte des Rechtecks verschoben hat (einschließlich Klick auf "Punkt fixieren"), sieht der Grafik-Bereich so aus:
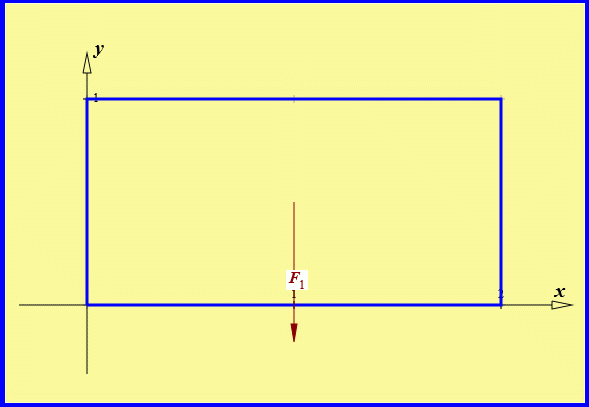
Nun kann "Gleichgewicht herstellen mit ... 3 Kräften" angeklickt werden, und es öffnet sich der Eingabebereich für die Definition der Wirkungslinien:

Eine Wirkungslinie wird durch die Koordinaten eines auf ihr liegenden Punktes und ihren Anstieg definiert. In dem Bildschirm-Ausschnitt sieht man die Zahlenwerte, die die drei Wirkungslinie der Aufgabenstellung erzeugen. Man sollte zunächst "Wirkungslinien zeichnen" wählen, um noch eventuell erforderliche Korrekturen vorzunehmen, danach liefert "Kräfte berechnen" folgendes Bild:
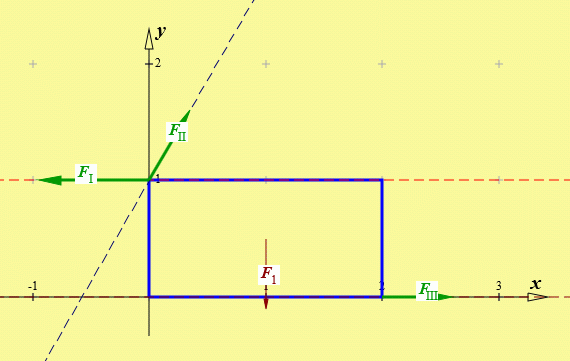
Und so sehen die Bereiche der Eingabe-Protokollierung und der Ergebnis-Ausgabe aus:

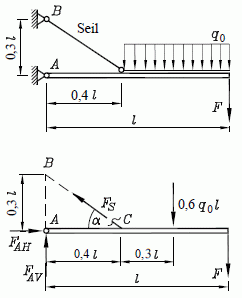
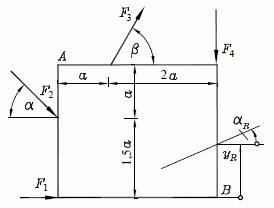
Beispiel 3: (Aufgabe entnommen aus dem Kapitel "Gleichgewicht des ebenen Kraftsystems" des Lehrbuchs "Dankert/Dankert: Technische Mechanik") Der skizzierte gerade Träger ist durch die Linienlast q0 und die Einzelkraft F belastet. Er ist bei A gelenkig gelagert und wird zusätzlich durch ein Seil gehalten.
Gegeben: l , q0 , F = 3q0l .Gesucht: Lagerkraft bei A und die Seilkraft.
Die Linienlast wird entsprechend nebenstehender Skizze durch eine Einzelkraft ersetzt. Für die Länge l und die Linienlast q0 werden (willkürlich) die Werte 1 angenommen, die Ergebnisse sind dementsprechend mit q0l zu multiplizieren.
Zur Orientierung (erforderlich ist das nicht) wird nach Klick auf "Polygon erzeugen" eine horizontale Linie vom Nullpunkt aus mit der Länge 1 gezeichnet und sofort mit "Polygon schließen" beendet. Klick auf "Zoom fit" zeigt nur noch den interessierenden Bereich. Um die wesentlichen Punkte erreichen zu können, sollten beide Rasterweiten und auch das Fangraster in beiden Richtungen auf 0.1 umgestellt werden. Der Grafik-Bereich sieht dann so aus:
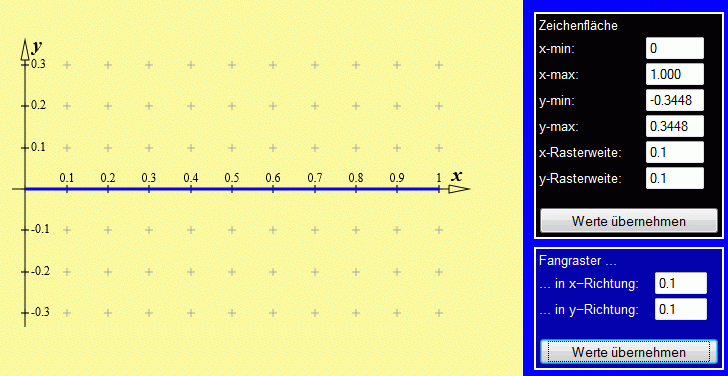
Die Eingabe der Kräfte ist über "Kraft und Winkel" oder über "Kraftkomponenten" möglich, zum Beispiel über F1 = 0.6 und α1 = −90° und Klick auf "Kraft und Winkel eingeben". Die hellblaue Spitze des erscheinenden Pfeils wird ("Drag and Drop") bis zum Punkt x = 0.7 verschoben und mit Klick auf "Punkt fixieren" verankert. Entsprechend wird die zweite Kraft als F2 = 3 und α3 = −90° und Klick auf "Kraft und Winkel eingeben" erzeugt. Nachdem der gelbe Fußpunkt des erscheinenden Pfeils bis zum Punkt x = 1 verschoben und dort fixiert wurde, sieht die Grafik so aus:
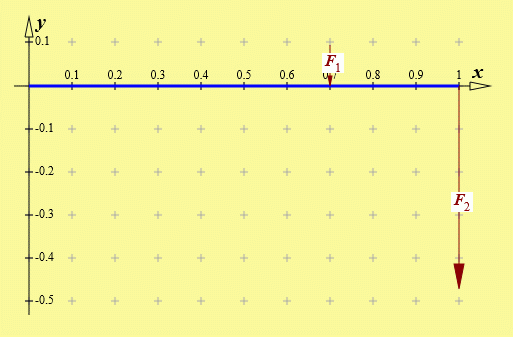
Nun kann zum Beispiel "Gleichgewicht herstellen mit ... zwei Kräften" angeklickt werden (natürlich ist auch "Gleichgewicht herstellen mit ... drei Kräften" möglich), und es öffnet sich der Eingabebereich für die Definition der Wirkungslinien:
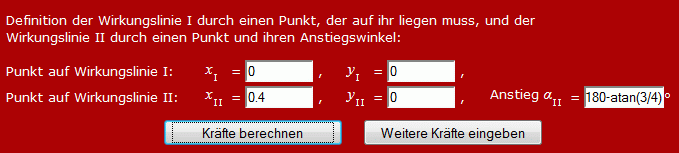
Die Felder sind schon entsprechend der Aufgabenstellung ausgefüllt: Für eine Wirkungslinie muss nur ein Punkt definiert werden (hier der Nullpunkt, wo sich das Festlager befindet). Die andere Wirkungslinie wird mit "Punkt und Anstieg" definiert. Man beachte, dass für den Anstiegswinkel mit 180−atan(3/4) ein arithmetischer Ausdruck eingegeben wurde, der vom Programm berechnet wird (dies ist für alle Eingabewerte möglich). Nun kann auf "Kräfte berechnen" geklickt werden, und die Ergebnisse erscheinen. Weil die berechneten Kräfte wesentlich größer sind als die gegebenen Kräfte, sind letztere in der Grafik kaum zu sehen. Es empfiehlt sich in diesem Fall, das "Häkchen" vor "Kräfte maßstäblich" zu entfernen. Danach sieht der Grafik-Bereich so aus:
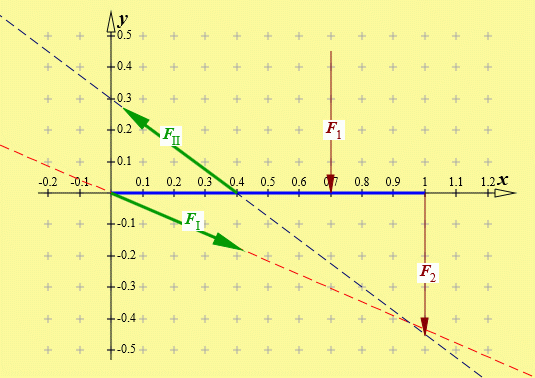
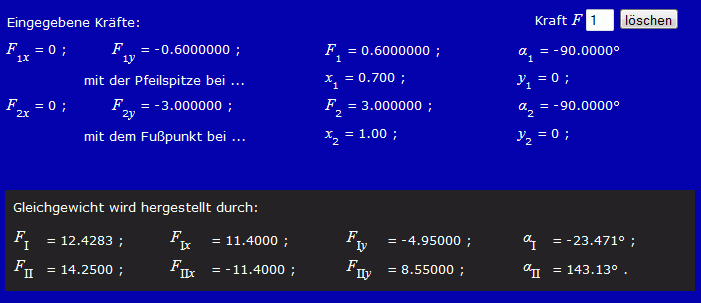
Das Eingabe-Protokoll und der Ergebnis-Bereich enthalten alle wesentlichen Informationen des behandelten Problems:
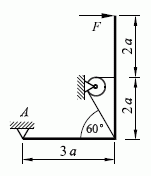
Beispiel 4: (Aufgabe entnommen aus dem Kapitel "Gleichgewicht des ebenen Kraftsystems" des Lehrbuchs "Dankert/Dankert: Technische Mechanik") Der skizzierte Hebel ist bei A gelenkig gelagert und wird zusätzlich durch ein über eine Umlenkrolle geführtes Seil gehalten.
Gegeben: a , F .Gesucht: Lagerkraft bei A und die Seilkraft.
Die Besonderheit dieser Aufgabe besteht darin, dass die Seilkraft am Hebel doppelt angreift. Es ist ein Fall für das Angebot "Gleichgewicht herstellen mit ... Kraft und Doppelkraft". Bei der Definition der Wirkungslinien für die beiden gleich großen Seilkräfte muss im Gegensatz zu allen anderen Angeboten in diesem Fall die Angabe der Winkel "passen", am besten so, dass die Seilkraft immer positiv angenommen wird.
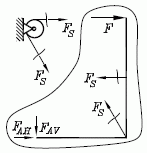
Die nebenstehende Schnittskizze, die man sich in dieser Form für die "Handrechnung" anfertigen würde, zeigt, was empfehlenswert ist: Die Wirkungsline am oberen Angriffspunkt des Seils wird mit dem Winkel 180° definiert, die Wirkungslinie am unteren Angriffspunkt mit dem Winkel 120°.
Für die Länge a wird (willkürlich) der Wert 1 angenommen, zur Orientierung (erforderlich ist das nicht) wird der Hebel gezeichnet und "Zoom ... fit" angeklickt. Die (auch als Einheitslast angenommene) Kraft F = 1 wird entweder als F1 = 1 und α1 = 0° und Klick auf "Kraft und Winkel eingeben" definiert oder aber über F1x = 1 und F1y = 0 und Klick auf "Kraftkomponenten eingeben". Nachdem man die (hellblaue) Pfeilspitze der Kraft an ihren Angriffspunkt verschoben hat (einschließlich Klick auf "Punkt fixieren"), sieht der Grafik-Bereich so aus:
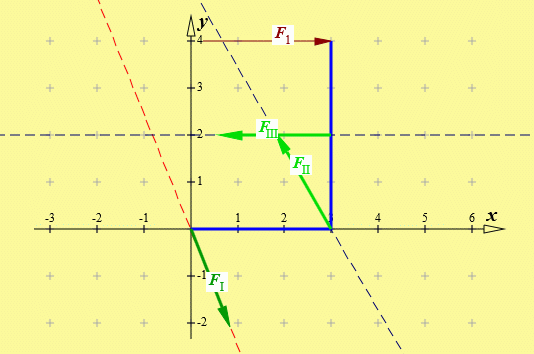
Nun kann "Gleichgewicht herstellen mit ... Kraft und Doppelkraft" angeklickt werden, und es öffnet sich der Eingabebereich für die Definition der Wirkungslinien:

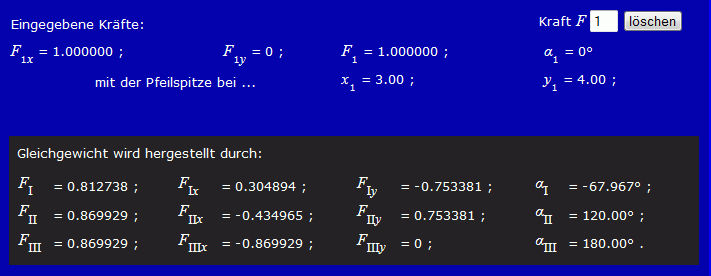
Für die Wirkungslinie durch den Punkt A müssen nur die Koordinaten dieses Punktes angegeben werden, bei der Definition der Wirkungslinien für die beiden Seilkräfte werden die oben gegebenen Bedingungen für die Angabe der Winkel eingehalten. In dem Bildschirm-Ausschnitt sieht man die Zahlenwerte, die die drei Wirkungslinie der Aufgabenstellung erzeugen. Anklicken von "Kräfte berechnen" liefert folgendes Bild:
Und so sehen die Bereiche der Eingabe-Protokollierung und der Ergebnis-Ausgabe aus:
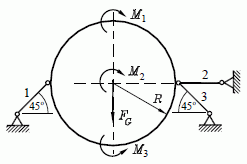
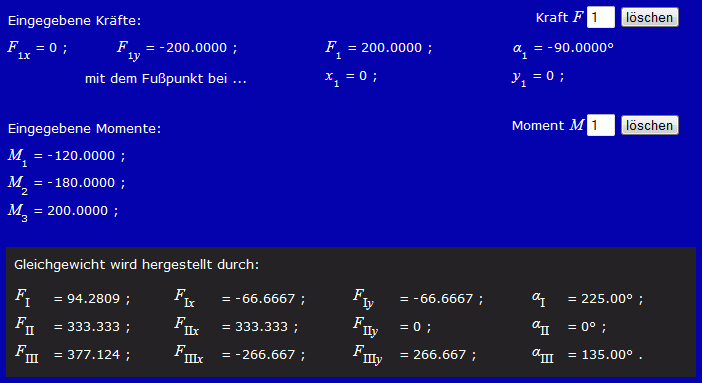
Beispiel 5: (Aufgabe entnommen aus dem Kapitel "Gleichgewicht des ebenen Kraftsystems" des Lehrbuchs "Dankert/Dankert: Technische Mechanik") Eine starre Kreisscheibe ist durch ihre im Mittelpunkt angreifende Eigengewichtskraft und die Momente M1, M2 und M3 belastet.
Gegeben: M1 = 120 Nm ; M2 = 180 Nm ; M3 = 200 Nm ; FG = 200 N ; R = 0,3 m .Gesucht: Stabkräfte in den Stäben 1, 2 und 3.
Weil die Abmessung der starren Scheibe wesentlich von den Voreinstellungen der Zeichenfläche abweicht, empfiehlt sich eine entsprechende Anpassung der Zeichenfläche einschließließlich der Rasterweiten und des Fangrasters. Zur besseren Orientierung wird auch hier ein Polygon gezeichnet. Weil ein Kreis nicht möglich ist, wird ein Quadrat gezeichnet. Danach könnte die Zeichenfläche zum Beispiel so aussehen:
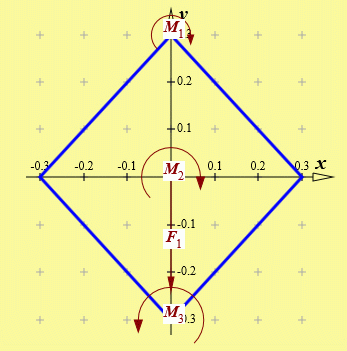
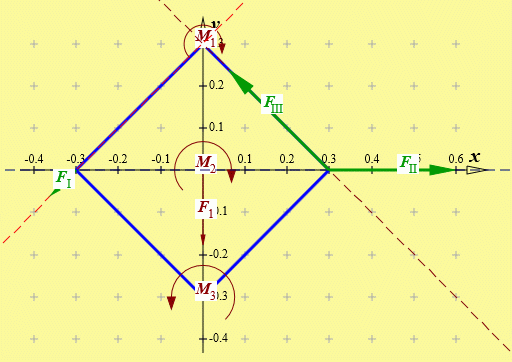
Die Eingabe der Gewichtskraft kann z. B. über F1 = 200 und α1 = −90 und Klick auf "Kraft und Winkel eingeben" realisiert werden. Die Eingabe der Momente könnte man vereinfachen (Momente sind in der Ebene frei verschiebbar), indem man die drei Momente zu einem (rechtsdrehenden) Moment MR = 100 Nm zusammenfasst. Hier wurden die drei Momente nicht nur einzeln eingegeben, sondern auch (was auch entbehrlich wäre) zu den Punkten verschoben, wie sie in der Aufgabenstellung gezeichnet waren. Nebenstehend sieht man die Zeichenfläche nach Eingabe der Belastung.
Nun wird "Gleichgewicht herstellen mit ... 3 Kräften" angeklickt. Die Wirkunglinien der unbekannten Kräfte werden jeweils mit den Koordinaten eines Punktes und dem Anstiegswinkel definiert. Im nachfolgenden Bildschirm-Ausschnitt sind schon die dafür erforderlichen Werte eingetragen:

Es empfiehlt sich, zunächst "Wirkungslinien zeichnen" zu wählen, um eventuell erforderliche Korrekturen vornehmen zu können. Danach wird "Kräfte berechnen" gewählt, und die Zeichenfläche sieht so aus:
Und so sehen die Bereiche der Eingabe-Protokollierung und der Ergebnis-Ausgabe aus: