... öffnet in einem separaten Fenster den Text in der Hilfe-Datei, der das Verfahren beschreibt, auf dem das Programm für die Berechnung der Eigenschwingungen ebener Rahmen beruht.
Die Seite startet mit einem Beispiel: Animation der zur 4. Eigenfrequenz gehörenden Schwingungsform eines speziellen Rahmens. Man kann die Animation stoppen (roter Button neben der Zeichenfläche), andere Schwingungsformen anzeigen lassen, das Modell ändern oder löschen (roter Button "Alles löschen"), um ein neues Modell zu definieren.
 
Aktuelle Maus-
koordinaten:
x =
y =
... zeigt einen kleineren Ausschnit (mit vergrößertem Modell).
... zeigt einen größeren Ausschnit (mit verkleinertem Modell).
... passt das gesamte Modell optimal in das Grafikfenster ein.
Verschiebung:
   
   
Ändern des Bildausschnitts
Zeichnen des Koordinatensystem ja/nein
Zeichnen des Rasters ja/nein
Anzeige der Knotennummern ja/nein (keine Anzeige bei Animation und Zeichnen der Schwingungsform)
Anzeige der Elementnummern (Elemente und Federelemente) ja/nein (keine Anzeige bei Animation und Zeichnen der Schwingungsform)
Koordinaten
Raster
Knoten-Nrn.
Elem.-Nrn.
Für alle Längen gilt die Dimension

.
Ändern des Bildausschnitts
Die hier eingestellte Längendimension gilt für alle Knoten (und damit automatisch für alle anderen Elemente)

Ihr Browser kann diese Grafik leider nicht darstellen. Die dafür erforderliche Unterstützung der Canvas-Grafik wird außer vom Internet Explorer von allen modernen Browsern (Mozilla, Chrome, Safari, Opera, Android, ...) seit vielen Generationen unterstützt. Der Internet Explorer unterstützt diese Grafik erst ab Version 9. Falls Sie (wie zu vermuten ist) eine ältere Internet-Explorer-Version benutzen, sollte dies der Anlass sein, ein Update auf die aktuelle Version zu starten (gegebenenfalls auch einen anderen Browser zu installieren).
Zeichenfläche
x-min:
x-max:
y-min:
y-max:
x-Rasterweite:
y-Rasterweite:
Die Einstellung der Grenzen der Zeichenfläche und des Rasters dienen gemeinsam mit der Darstellung des Koordinatensystems ausschließlich zur Orientierung, können jederzeit geändert werden. Die für die Längen geltende Dimension wird durch die Einstellung links unten neben der Zeichenfläche geregelt. Das Raster in der Zeichenfläche ist unabhängig vom Fangraster.
Fangraster ...
... in x−Richtung:
... in y−Richtung:
Fangraster: Mit den beiden Werten wird ein (nicht sichtbares) Netz definiert, auf dessen Schnittpunkte die Mauskoordinaten innerhalb der Zeichenfläche gefangen werden (siehe Anzeige "Aktuelle Mauskoordinaten" links oben). Punkte, die nicht auf dem Raster liegen, können über die Tastatur eingegeben werden.
Berechnet werden die Eigenfrequenzen und die Eigenschwingungsformen für ebene biege- und dehnsteife Rahmen. Die Eigenschwingungsformen können grafisch dargestellt und die Schwingungen als Animation visualisiert werden.
Eingabe starten mit Klick auf eines der folgenden Angebote:
     
Nach Anklicken dieses Buttons können beliebig viele Elemente (biege- und dehnsteif) definiert werden. Dafür sind zwei Knoten (Mausklick in Grafikbereich oder Tastatureingabe), Biegesteifigkeit, Dehnsteifigkeit und Massebelegung (Masse pro Länge) einzugeben.
Nach Anklicken dieses Buttons können beliebig viele Federelemente definiert werden. Dafür sind zwei Knoten (Mausklick in Grafikbereich oder Tastatureingabe) und die Federzahl einzugeben. Federelemente liegen zwischen zwei Knoten der Struktur (im Gegensatz zu Federlagern, mit denen ein Knoten elastisch gelagert wird).
Nach Anklicken dieses Buttons können beliebig viele Knoten definiert werden (Mausklick in Grafikbereich oder Tastatureingabe). Dieses Angebot sollte nur genutzt werden, wenn die Knoten eine bestimmte Nummerierung erhalten sollen, ansonsten entstehen Knoten automatisch bei Definition aller anderen Elemente.
Ändern und löschen:

Gelbe Buttons gestatten das Löschen bzw. Ändern der entsprechenden Elemente.
... öffnet ein separates Fenster mit ausführlicher Beschreibung aller Funktionen.
... berechnet die Eigenfrequenzen und Eigenschwingungsformen des Systems.
... löscht alle Komponenten des eingegebenen Modells.
... überprüft das eingegebene Modell auf Vollständigkeit und gegebenenfalls auf Erfüllung der formalen Bedingung für die statische Bestimmtheit des Systems.
   
 
    
 
 
 
     
Festlager: Nach Anklicken eines Buttons können beliebig viele Lager dieses Typs definiert werden. Die 4 Angebote unterscheiden sich nur optisch, alle Lager verhindern Verschiebungen in beliebiger Richtung.
Loslager: Nach Anklicken eines Buttons können beliebig viele Lager dieses Typs definiert werden. Die beiden Angebote unterscheiden sich nur optisch, sie verhindern beide die Verschiebung in vertikaler Richtung.
Loslager: Nach Anklicken eines Buttons können beliebig viele Lager dieses Typs definiert werden. Die beiden Angebote unterscheiden sich nur optisch, sie verhindern beide die Verschiebung in horizontaler Richtung.
Starre Einspannung: Nach Anklicken eines Buttons können beliebig viele Lager dieses Typs definiert werden. Die 4 Angebote unterscheiden sich nur optisch, sie verhindern alle die Verschiebung in beliebiger Richtung, außerdem kann sich kein Biegewinkel einstellen.
Elastisches Lager: Nach Anklicken eines Buttons können beliebig viele Lager dieses Typs definiert werden. Die beiden Angebote unterscheiden sich nur optisch, sie leiten beide eine Kraft in horizontaler Richtung am Knoten (schwarzes Quadrat) ein, die proportional zur horizontalen Verschiebung an diesem Punkt ist (Proportionalitätsfaktor: Federzahl c).
Elastisches Lager: Nach Anklicken eines Buttons können beliebig viele Lager dieses Typs definiert werden. Die beiden Angebote unterscheiden sich nur optisch, sie leiten beide eine Kraft in vertikaler Richtung am Knoten (schwarzes Quadrat) ein, die proportional zur vertikalen Verschiebung an diesem Punkt ist (Proportionalitätsfaktor: Federzahl c).
Elastisches Lager (Drehfeder): Nach Anklicken des Buttons kann ein Lager definiert werden, das ein Moment am Knoten (schwarzes Quadrat) einleitet, das proportional zum Biegewinkel an diesem Punkt ist (Proportionalitätsfaktor: Drehfederzahl cT).
Knotenmasse: Nach Anklicken des Buttons kann eine Masse definiert werden, die an einem Knoten platziert wird. Diese kann punktförmig sein (Masse m), jedoch auch mit Drehträgheit versehen werden (Massenträgheitsmoment Izz).
 

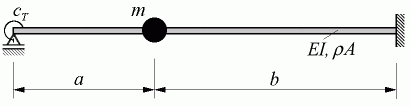
Beispiel 1: Für den skizzierten Träger mit konstantem Querschnitt sind die 3 kleinsten Eigenfrequenzen der Biegeschwingungen und die zugehörigen Schwingungsformen zu ermitteln (die Masse m soll eine Punktmasse sein).

Gegeben:    EI = 5·109 Nmm2 ;  ρA = 4,8 kg/m ;  m = 4 kg ;
  a = 600 mm ;  b = 800 mm ;  cT = 60 kNm .

Zunächst wird eine besonders grobe Einteilung in nur zwei Elemente realisiert, mit der man in der Regel nur die 1. Eigenfrequenz ausreichend genau berechnen kann. Das Erzeugen des Berechnungsmodells wird auf der Seite Beispiel 1 "Schritt für Schritt" beschrieben. Man kann das Berechnungsmodell allerdings auch hier mit Klick auf nebenstehenden Button automatisch aufbauen und berechnen lassen (im Grafik-Fenster oben startet dann gleich die Animation der 1. Eigenschwingungsform).

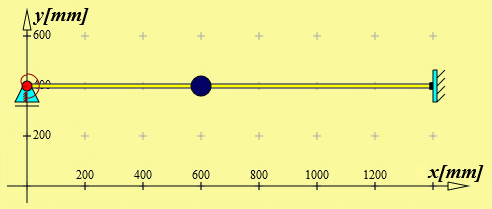
Nebenstehend sieht man das komplette Berechnungsmodell für die Einteilung in nur 2 Elemente. Die mit diesem Modell berechnet 1. Eigenfrequenz f1 = 34,478 s−1 weicht vom exakten Wert (siehe: Analytische Lösung) um weniger als 0,3% ab, die Näherung der 2. Eigenfrequenz durch dieses Modell ist allerdings schon unbrauchbar.

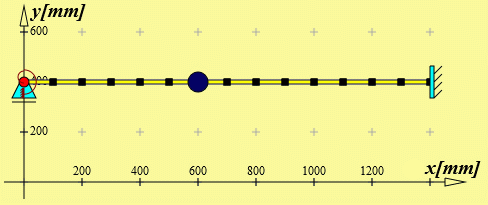
Es wird deshalb noch ein verfeinertes Modell erzeugt. Auch das Erzeugen dieses (nebenstehend zu sehenden) Modells wird auf der Seite Beispiel 1 "Schritt für Schritt" beschrieben. Man kann das feinere Berechnungsmodell allerdings auch hier mit Klick auf nebenstehenden Button automatisch aufbauen und berechnen lassen (im Grafik-Fenster oben startet dann gleich die Animation der 1. Eigenschwingungsform).

Mit diesem Modell erhält man Ergebnisse, die auch für die höheren Eigenfrequenzen brauchbar sind:

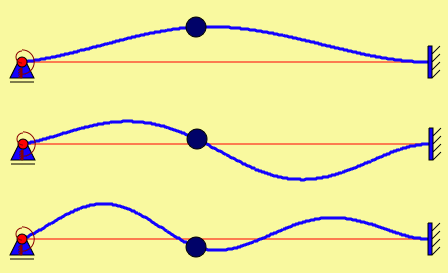
Zum Vergleich: Die recht aufwendige exakte Lösung wird hier demonstriert. Für die ersten drei Eigenfrequenzen findet man dort: f1 = 34,381 s−1, f2 = 144,01 s−1, f3 = 255,08 s−1.

Die mit 14 Elementen berechneten Frequenzen sind praktisch exakt, damit auch die zugehörigen Schwingungsformen. Nebenstehend sieht man die zu den ersten drei Eigenfrequenzen gehörenden Schwingungsformen.

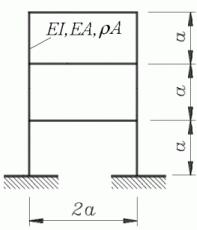
Beispiel 2: Für den skizzierten biege- und dehnsteifen Rahmen mit konstantem Querschnitt berechne man die kleinsten Eigenkreisfrequenzen und die zugehörigen Eigenschwingungsformen.

Gegeben:    EI = 3,5·106 Nm2 ;  EA = 2,9·109 N ;  ρA = 100 kg/m ;  a = 2 m .

Das Erzeugen des Berechnungsmodells wird auf der Seite Beispiel 2 "Schritt für Schritt" beschrieben. Man kann das Berechnungsmodell allerdings auch hier mit Klick auf nebenstehenden Button automatisch aufbauen und berechnen lassen (im Grafik-Fenster oben startet dann gleich die Animation der 1. Eigenschwingungsform).

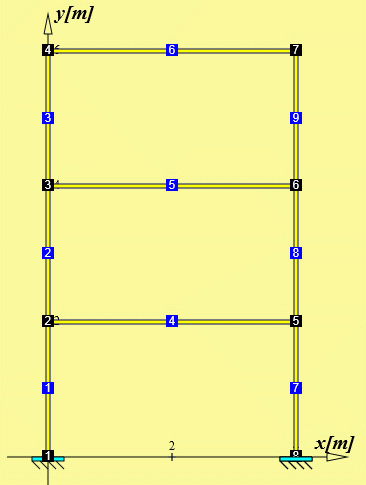
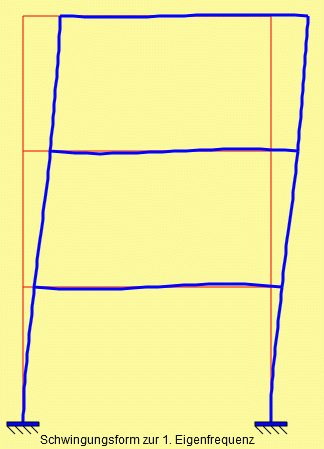
Nebenstehend links sieht man das komplette Berechnungsmodell mit 9 Elementen. Die zur 1. Eigenfrequenz gehörende Schwingungsform ist nebenstehend rechts zu sehen.

Beispiel 3: Für Schwingungsberechnungen ist es nicht erforderlich, dass das System so gelagert ist, dass es im Sinne der Statik tragfähig wäre. Beim Start dieser Seite ist ein Beispiel zu sehen, das in horizontaler Richtung nicht fixiert ist.

Für solche Systeme ist eine Starrkörperbewegung möglich, die sich bei der Eigenschwingungsberechnung durch mindestens eine Eigenkreisfrequenz ω = 0 bemerkbar macht. Diese "Schwingungen" werden vom Programm aussortiert, deshalb wird als Grundfrequenz für den Rahmen die zur nebenstehend zu sehenden Schwingungsform gehörende Frequenz ausgewiesen.

In der Ebene sind maximal drei Starrkörperbewegungen möglich. Am nebenstehend zu sehenden Biegeträger ohne jegliche Lagerung soll das demonstriert werden. Das Berechnungsmodell kann mit Klick auf den nachfolgenden Button geladen werden. Es nähert (sehr grob) einen Speer an, wie er beim Speerwerfen (Männer) verwendet wird: Zumindest die Gesamtmasse und die Gesamtlänge stimmen.

Die Schwingungsformen, die nebenstehend zu sehen sind, entsprechen denen, die man bei Leichtathletik-Übertragungen von Speerwurf-Wettbewerben gelegentlich sehen konnte, wenn der Speer mit einer Zeitlupenaufnahme verfolgt wurde.

Beispiel 4: Mit dem Programm können auch Feder-Masse-Schwinger berechnet werden. Nebenstehend sieht man einen einfachen Zwei-Massen-Schwinger, für den im Kapitel "Systeme mit mehreren Freiheitsgraden" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" für die beiden Eigenkreisfrequenzen die exakten Werte

berechnet werden. Rechts sieht man das Modell, das mit dem hier verfügbaren Programm erzeugt wurde: 2 Knotenmassen, 3 Federelemente und 4 Lager. Man kann das Modell mit Klick auf den folgenden Button laden und im Grafikbereich oben die Schwingung verfolgen.

Mit den Zahlenwerten m = 1 kg für die beiden Massen und c = 1 N/m erhält man die folgenden (exakten) Ergebnisse:

Home Homepage TM-aktuell       Home Homepage TM-Mathe       Home Homepage TM:Ergänzung/Vertiefung       facebook Dankerts TM auf facebook