Symmetrisches Matrizeneigenwertproblem

Beispiel 1: Im Kapitel 19 des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird folgende Aufgabe formuliert:

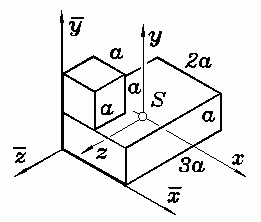
Für den aus einem Quader und einem Würfel zusammengesetzten homogenen Körper sollen die Lage der Hauptzentralachsen und die zugehörigen Hauptträgheitmomente ermittelt werden.

Gegeben:  a ,  Dichte ρ .

Nach einigen (recht mühsamen) Vorarbeiten (Berechnung der Lage des Schwerpunkts und Berechnung aller Trägheitsmomente bezüglich des eingezeichneten Schwerpunktkoordinatensystems) kann der Trägheitstensor bezüglich des x-y-z-Koordinatensystems aufgeschrieben werden (enthät die drei Massenträgheitsmomente J_xx, J_yy und J_zz und die drei Deviationsmomente J_xy, J_xz und J_yz):

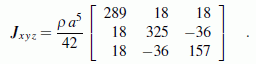
Die Eigenwerte dieser Matrix sind die Hauptträgheitmomente, ihre Eigenvektoren definieren die Lage der Hauptzentralachsen. Hier findet man die komplette Rechnung mit dem Programm "Symmetrisches Matrizeneigenwertproblem".

Beispiel 2: Im Kapitel 32 des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird folgende Aufgabe formuliert:

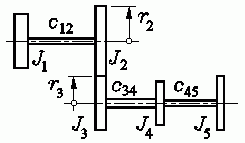Für das skizzierte Getriebe mit fünf (starren) Rädern und drei (masselosen) Torsionsfedern (Wellenabschnitte) soll das Matrizeneigenwertproblem für die Berechnung der Eigenkreisfrequenzen der Torsionsschwingungen formuliert werden. Es darf vorausgesetzt werden, dass die beiden Zahnräder mit den Massenträgheitsmomenten J₂ und J₃ und den Teilkreisradien r₂ und r₃ spielfrei miteinander kämmen.

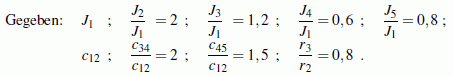
Das Schwingungs-Differenzialgleichungssystem führt nach nicht sehr schwieriger Rechnung auf folgendes Matrizeneigenwertproblem:

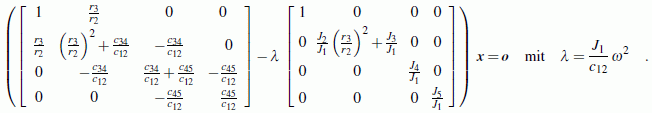
Die Eigenwerte dieses allgemeinen Matrizeneigenwertproblems sind also dem Quadrat der Eigenkreisfrequenzen proportional. Hier findet man die komplette Rechnung mit dem Programm "Symmetrisches Matrizeneigenwertproblem".

Beispiel 3: Im Kapitel 23 des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird folgende Aufgabe formuliert:

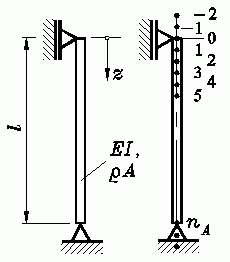
Der skizzierte Stab ist nur durch sein Eigengewicht belastet. Es soll ermittelt werden, bei welcher kritischen Länge er allein durch die Eigengewichts-Belastung knickt.

Gegeben:   EI ,   Dichte ρ ,   Querschnittsfläche A .

Die Lösung wird mit dem Differenzenverfahren erreicht: Der Stab wird in n_A äquidistante Abschnitte unterteilt, es entstehen n_A − 1 Punkte im Inneren des Stabs, für die die Differenzenformeln aufgeschrieben werden. In diese Gleichungen gehen auch die Rand- und Außenpunkte ein, die mit Hilfe der Randbedingungen eliminiert werden können.

Dieser Weg wird im Lehrbuch ausführlich beschrieben. Nach etwas mühsamer (aber nicht sehr schwieriger) Rechnung entsteht ein Matrizeneigenwertproblem. Für n_A = 8 sieht es zum Beispiel so aus:

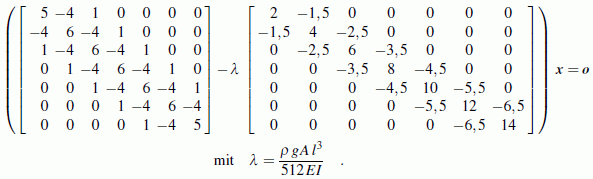
Nach der Lösung dieses Matrizeneigenwertproblems kann aus dem kleinsten Eigenwert die kritische Länge berechnet werden. Hier findet man die komplette Beschreibung der Lösung des Problems mit dem Programm "Symmetrisches Matrizeneigenwertproblem".

Beispiel 4: Ein weiteres Beispiel (Eigenschwingungen eines Biegeträgers mit der Finite-Elemente-Methode), das mit dem Programm "Symmetrisches Matrizeneigenwertproblem" berechnet wurde, findet man im Bereich "Mathematik für die Technische Mechanik" auf der Seite "Eigenschwingungen eines Biegeträgers".